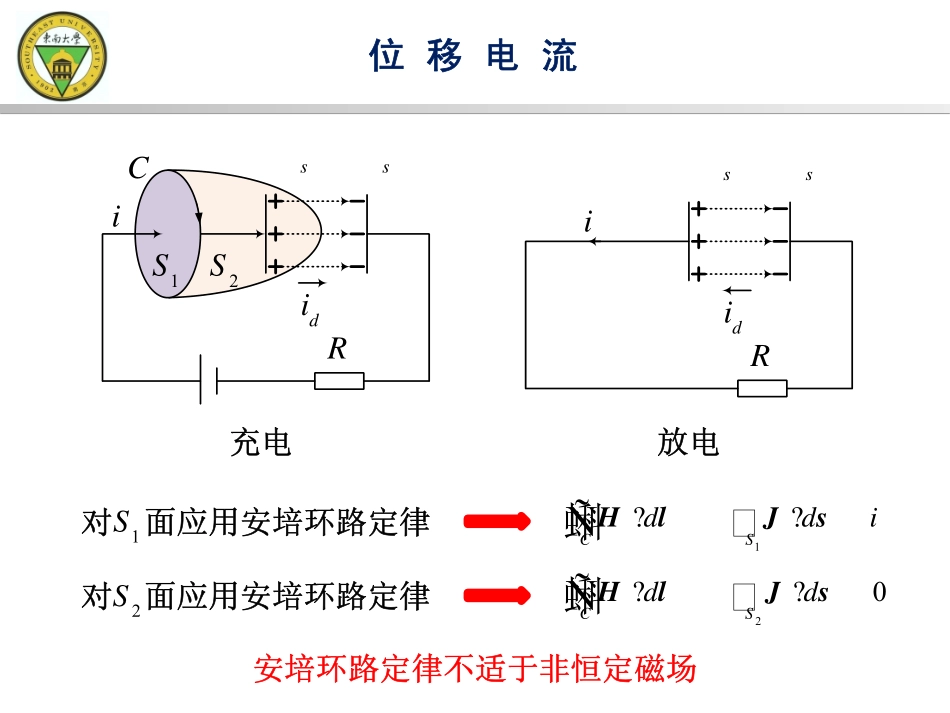
毫米波国家重点实验室信息科学与工程学院东南大学电磁场与电磁波第五章时变电磁场位移电流1S2SssidiRCssidiR1CSddi??蝌�HlJsÑ20CSdd??蝌�HlJsÑ充电放电对面应用安培环路定律1S对面应用安培环路定律2S安培环路定律不适于非恒定磁场�设极板面积为,若充放电某一时刻极板上的电量和面电荷密度分别为和,则导线内的传导电流满足�极板间电通量随时间的变化率为�电位移矢量的大小随时间的变化率为方向上,充电时与极板间电场强度方向一致,放电时相反。显然,具有电流密度的量纲。位移电流sddqiSdtdtr==sdJdtr=Sqsr()esdSDddSidtdtdtYr===sdddDJdtdtdtr===DddtDddtD�麦克斯韦引入了位移电流的概念,他定义:穿过电场中某一截面的电通量随时间的变化率为通过该截面的位移电流强度,即而电场中某一点的电位移矢量随时间的变化率为该点位移电流密度,即�通过引入位移电流,并用它们代替极板间中断的电流,则整个回路电流连续。位移电流eddidtY=dt¶=¶JD位移电流不是电荷的运动,而是一种人为定义�根据电荷守恒定律和高斯定理,得其中称为全电流,为传导电流或运流电流,为位移电流。全电流在任何情况下都是连续的。全电流连续性定理tr¶炎=-¶J0tt骣¶÷ç÷炎+=炎=ç÷ç÷ç¶桫DJJr炎=D0tSSddt骣¶÷ç÷+??ç÷ç÷ç¶桫蝌蝌DJsJs乙td=+JJJJcJvJdJ�麦克斯韦认为位移电流也可产生磁场,安培环路定律可推广至时变场情况,即全电流定律�时变磁场由传导电流、运流电流和位移电流共同产生,而位移电流是由时变电场形成的,由此可见,时变电场可产生时变磁场。�电磁感应定律表明时变磁场可产生时变电场。因此,麦克斯韦引入位移电流后,预见到时变电场与时变磁场可以在空间中相互转化,进而形成电磁波。全电流定律CStdidt骣¶÷ç÷?=+�ç÷ç÷çè¶ø蝌�DHlJsÑtt¶汛==+¶DHJJ麦克斯韦方程t¶汛=+¶DHJt¶汛=-¶BE0炎=Br炎=DCSddt骣¶÷ç÷?+�ç÷ç÷ç桫¶蝌�DHlJsÑCStdd¶¶?-�蝌�BElsÑ0Sd?蝌BsÒSdq?蝌DsÒSVdddtdvr?-蝌蝌�JsÒtr¶炎=-¶J全电流定律电磁感应定律磁通连续性定理电荷守恒定律高斯定理①④③②⑤=cvisrìï=ï+íï=ïîvJJEJJe=DEm=BH本构关系积分形式微分形式�时变电场是有旋有散的,时变磁场是有旋无散的。但,时变电磁场中的电场与磁场是不可分割的,因此,时变电磁场是有旋有散场。�在无源区中,时变电磁场是有旋无散的。�电场线与磁场线相互交链,自行闭合,从而在空间形成电磁波。�静态场和恒定场是时变场的两种特殊形式。时变电磁场时变电磁场E边界条件SSlh211E2E2ˆl1ˆlˆnCStdd¶¶?-�蝌�BElsÑ()11221200ˆˆˆˆlimhCludllln®D轾D+D==犏ë=û-鬃�状òElEEEEÑ12ttEE=()120ˆn-=´EE任何边界上电场强度的切向分量连续时变电磁场D边界条件Sdq=×蝌DSÒ012ˆˆlimhSndSSnqD®=D-D=鬃×蝌DDDSÒ()12ˆsnr-=×DDSShˆn211D2D12nnsDDr-=除导体外,任何边界上电位移矢量的法向分量连续时变电磁场H边界条件SDSlD2m1m1H2H2ˆl1ˆlˆnCSddt骣¶÷ç÷?+�ç÷ç÷ç桫¶蝌�DHlJsÑ()1122120ˆˆˆlimˆhlulIllndllD®轾D+D===-犏臌D状鬃�òHlHHHHÑ()12ˆsn-=´HHJ除理想导体外,任何边界上磁场强度的切向分量连续时变电磁场B边界条件0Sd=×蝌BSÒ0120ˆˆlimhSndSnS®D=D-D=鬃×蝌BSBBÒ()120ˆn-=×BBSShˆn211B2B12nnBB=任何边界上磁感应强度的法向分量连续�理想导电体内部不可能存在时变电磁场及时变的传导电流,它们只可能分布在理想导电体的表面。�理想导电体表面支持面电流和面电荷分布,此时,磁场强度的切向分量和电位移矢量的法向分量不再连续。理想导体的边界条件SED0tttEHJHB0tE=nsDr=ˆsn?HJ0nB=0¹Es==¥JE0¹H0¹E0¹J0¹H�根据麦克斯韦方程,简单媒质中:由矢量微分恒等式并利用和,得时变电磁场的位方程及其解22tme¶汛汛+=汛¶HHJ22ttmem抖汛汛+=-¶¶EJE()2汛汛=蜒?�AAA222tme¶?=-汛¶HHJ222ttrmeme抖�?=+¶¶EJE0炎=Br炎=D场源关系复杂,且两个方程相互耦合�引入标量位与矢量位可简化时变电磁场的求解。由,B可表示为矢量场A的旋度,即式中A称为矢量位,将上式代入得时变电磁场...