磁场部分 习题课VIP免费

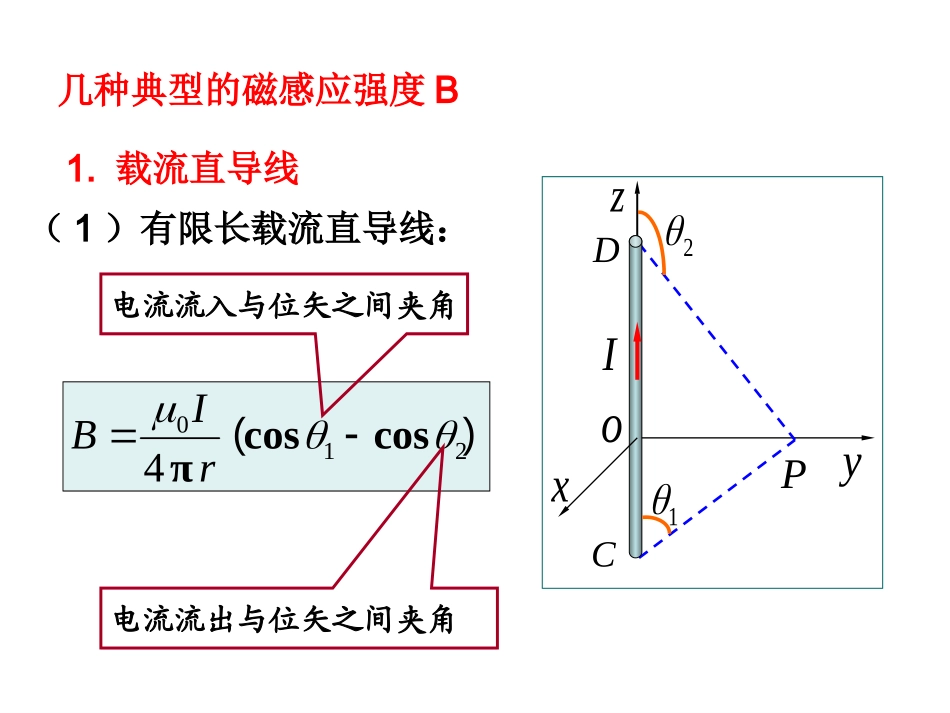
稳恒磁场习题课0dSSBniiLIlB10d一两个基本方程：1.磁场的高斯定理（磁通连续定理）磁场是无源场。2.安培环路定理磁场是非保守场。磁场性质：无源有旋。电场性质：有源无旋。——电流元在空间某场点P产生的磁感应强度dB30dπ4drrlIB二毕奥—萨伐尔定律任意载流导线在场点P处的磁感强度30dπ4drrlIBB几种典型的磁感应强度B1.载流直导线（1）有限长载流直导线：）（2104coscosπrIB电流流入与位矢之间夹角电流流出与位矢之间夹角12PCDyxzoI（a）无限长载流直导线：rIBπ20rIBπ40（b）半无限长载流直导线：（c）P点位于直导线延长线上：几种特殊情况B=02322202）（RxIRBRIB202）环心处0x1）若线圈有匝N2322202）（RxIRNBx*BxoRI3）Rx30320π22xISBxIRB，2.圆电流轴线上的磁场.o（2R）I+R（3）oIIRo（1）x0BRIB400半圆环中心RIB200圆环中心RIB800圆环中心41oI2R1R（5）*Ad（4）*1010200π444RIRIRIBdIBAπ403.长直载流螺线管FqBvnIB0内部：外部：B=0三磁力----三种1.洛伦兹力：运动的带电粒子在磁场中所受磁力qBmRvBvqBmTπ2mqBTπ21匀速圆周运动2.安培力（电流元在磁场中所受磁力）BlIFdd3、线圈受力----磁矩磁力矩磁力矩的功：neISm1.磁矩BmM2.磁力矩3.磁力矩的功ΦIWΔ五安培环路定理niiLIlB10d真空中存在磁介质时：iLIlHd一.已知电流分布，求磁感应强度二、已知磁感应强度，求磁场对电流和运动电荷的作用两类基本问题2.利用安培环路定理。1.利用磁场的叠加原理：毕奥－萨伐尔定律；两种方法：三种情况：运动带电粒子，载流导线，载流线圈：电流密度1.利用磁场的叠加原理求磁感应强度：毕奥－萨伐尔定律步骤:1.选取Idl，写出dB的大小，方向．2.建立坐标系，写出dB的分量式．3.统一积分变量，确定上下限，求积分求出Bx，By，Bz，写出合磁感应强度．2.利用安培环路定理求磁感应强度3.确定回路包围的电流，求得B的大小步骤:1.分析磁场分布的对称性；2.作适当的闭合回路L，确定L绕向(积分路径走向)；条件：只有电流分布（磁场分布）具有对称性时才可利用安培环路定理求磁感应强度。例1.一无限长圆柱形导体(磁导率μ0),半径为R,通有均匀电流I。今取一矩形平面S(长为1m,宽为2R),如图中斜线阴影部分所示,求通过该矩形平面的磁通量。解：本题的电流分布满足安培环路定理求磁场的条件，由安培环路定理易求得圆柱体内外的磁感应强度值为RrrIRrrRIB,2,2020在离圆柱体轴线r处的斜线平面上取宽dr的面积条，其磁通量为rBSBd1ddrBddRRRrrIrrRI20020d2d2解图5-A-19R2IS1mrdrdS22400lnIIRo解圆电流的磁场rrrrTdqId2dπ2drrIBd22dd00例2半径为的带电薄圆盘的电荷面密度为,并以角速度绕通过盘心垂直于盘面的轴转动，求圆盘中心的磁感强度.Rrrd2d2000RrBR例3电流均匀地流过宽为b的无限长平面导体薄板,电流为I,沿板长方向流动.求(1)在薄板平面内,距板的一边为b的P点处的磁感应强度[图(a)];(2)通过板的中线并与板面垂直的直线上一点Q处的磁感应强度,Q点到板面的距离为x[图(b)].分析:宽为b的无限长载流导体薄板可视为由宽为dy的无限长载流细条平行排列而成.每个细条的电流为ybIIdd平板在空间任一点P处的磁感应强度dB可利用无限长载流直导线的磁感应强度规律求得.解:(1)建立坐标系.（2）取宽为dy、载流为dI的细条在P点磁感应强度yybbIybbIBd)23(2)2(2dd00方向垂直纸面向里.由于所有细条在P点处的磁感应强度方向相同,因而整块载流导体薄板在P点的磁感应强度的大小为2ln223d2d0220bIybybIBBbb方向垂直纸面向里.(2)建立坐标系如解图(b)所示,载流的细条,在Q点处的磁感应强度的大小为ybIIddyrbIrIBd22dd00方向与r垂直,在平面内.xOysinddBB...