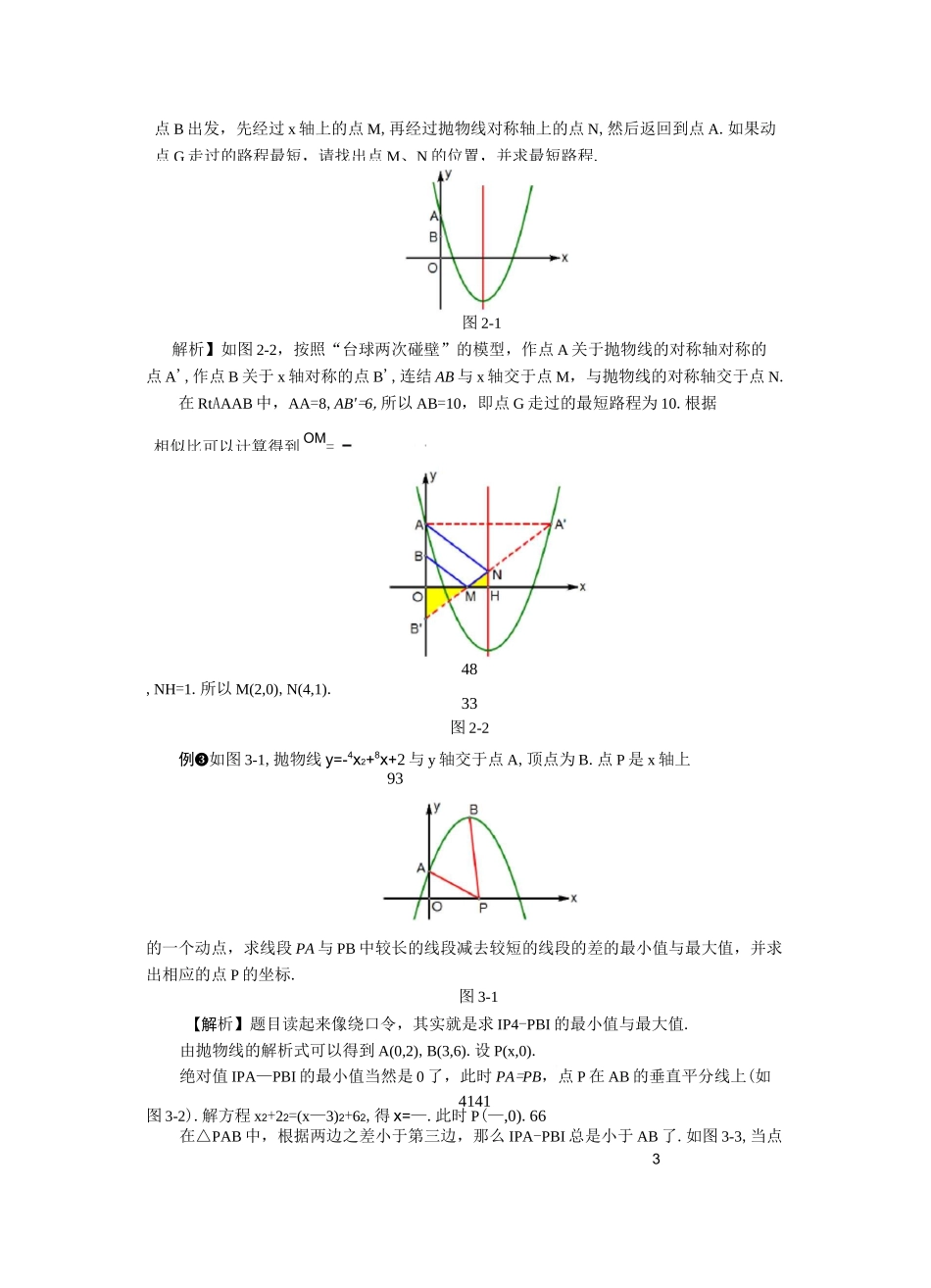
图1-3中考数学压轴题解题策略(8)线段和差最值的存在性问题解题策略专题攻略两条动线段的和的最小值问题,常见的是典型的“牛喝水”问题,关键是指出一条对称轴“河流”(如图1).三条动线段的和的最小值问题,常见的是典型的“台球两次碰壁”或“光的两次反射”问题,关键是指出两条对称轴“反射镜面”(如图2).两条线段差的最大值问题,一般根据三角形的两边之差小于第三边,当三点共线时,两条线段差的最大值就是第三边的长•如图3,PA与PB的差的最大值就是AB,此时点P在AB的延长线上,即P.例题解析图1-2例❷如图,抛物线y=2x2-4x+4与y轴交于点A,B是OA的中点.一个动点G从A蓋牛BNEM牛H解决河例❶如图1-1,抛物线y=x2—2x—3与x轴交于A、B两点,与y轴交于点C,点P是抛物线对称轴上的一个动点,如果APAC的周长最小,求点P的坐标.图1-1【解析】如图1-2,把抛物线的对称轴当作河流,点A与点B对称,连结BC,那么在△PBC中,PB+PC总是大于BC的.如图1-3,当点P落在BC上时,PB+PC最小,因此PA+PC最小,APAC的周长也最小.由y=x2-2x-3,可知OB=OC=3,OD=1.所以DB=DP=2,因此P(1,—2).图2-1解析】如图2-2,按照“台球两次碰壁”的模型,作点A关于抛物线的对称轴对称的点A',作点B关于x轴对称的点B',连结AB与x轴交于点M,与抛物线的对称轴交于点N.在RtAAAB中,AA=8,AB'=6,所以AB=10,即点G走过的最短路程为10.根据48,NH=1.所以M(2,0),N(4,1).33图2-2例❸如图3-1,抛物线y=-4x2+8x+2与y轴交于点A,顶点为B.点P是x轴上93的一个动点,求线段PA与PB中较长的线段减去较短的线段的差的最小值与最大值,并求出相应的点P的坐标.图3-1【解析】题目读起来像绕口令,其实就是求IP4-PBI的最小值与最大值.由抛物线的解析式可以得到A(0,2),B(3,6).设P(x,0).绝对值IPA—PBI的最小值当然是0了,此时PA=PB,点P在AB的垂直平分线上(如4141图3-2).解方程x2+22=(x—3)2+62,得x=—.此时P(—,0).66在△PAB中,根据两边之差小于第三边,那么IPA-PBI总是小于AB了.如图3-3,当点3点B出发,先经过x轴上的点M,再经过抛物线对称轴上的点N,然后返回到点A.如果动点G走过的路程最短,请找出点M、N的位置,并求最短路程.相似比可以计算得到OM=P在BA的延长线上时,IPA-PBI取得最大值,最大值AB=5.此时P(-2,0).例❹如图4-1,菱形ABCD中,AB=2,ZA=120。,点P、Q、K分别为线段BC、CD、BD上的任意一点,求PK+QK的最小值.【解析】如图4-2,点Q关于直线BD的对称点为Q,在厶KPQ中,PK+QK总是大于PQ'的.如图4-3,当点K落在PQ上时,PK+QK的最小值为PQ'.如图4-4,PQ'的最小值为QH,QH就是菱形ABCD的高,Q3.这道题目应用了两个典型的最值结论:两点之间,线段最短;垂线段最短.图4-2图4-3图4-4例❺如图5-1,菱形ABCD中,ZA=60°,AB=3,OA>OB的半径分别为2和1,P、E、F分别是边CD、OB和OA上的动点,求PE+PF的最小值.图5-1【解析】E、F、P三个点都不确定,怎么办?BE=1,AF=2是确定的,那么我们可以求PB+PA-3的最小值,先求PB+PA的最小值(如图5-2).如图5-3,PB+P4的最小值为AB',ABf=6.所以PE+PF的最小值等于3.图6-如图6-2,将线段BF向左平移两个单位,得到线段ME.如图6-3,作点A关于x轴的对称点A',MA'与x轴的交点E,满足AE+ME最小.由△AOE“BHF,得祭=HB.解方程2=斗,得a=!•图6-2例❼如图7-1,^ABC中,ZACB=90°,AC=2,BC=1.点A、C分别在x轴和y轴的正半轴上,当点A在x轴上运动时,点C也随之在y轴上运动.在整个运动过程中,图5-2图5-3例❻如图6-1,已知A(0,2)、B(6,4)、E(a,0)、F(a+1,0),求a为何值时,四边形ABEF周长最小?请说明理由.图6-1【解析】在四边形ABEF中,AB、EF为定值,求AE+BF的最小值,先把这两条线段图7-1【解析】如果把OB放在某一个三角形中,这个三角形的另外两条边的大小是确定的那么根据两边之和大于第三边,可知第三边OB的最大值就是另两边的和.显然AOBC是不符合条件的,因为OC边的大小不确定.如图7-2,如果选AC的中点D,那么BD、OD都是定值,OD=1,BD=迈.在AOBD中,总是有OBVOD+BD.如图7-3,当点D落在OB上时,OB最大,最大值为叮2+1.图7-2图7-3例❽如图8-1,已知A(—2,0)、B(4,0)、D(-5,3朽).设F为线段BD上一点(不含端点),连结AF...