平行线的判定课件VIP免费

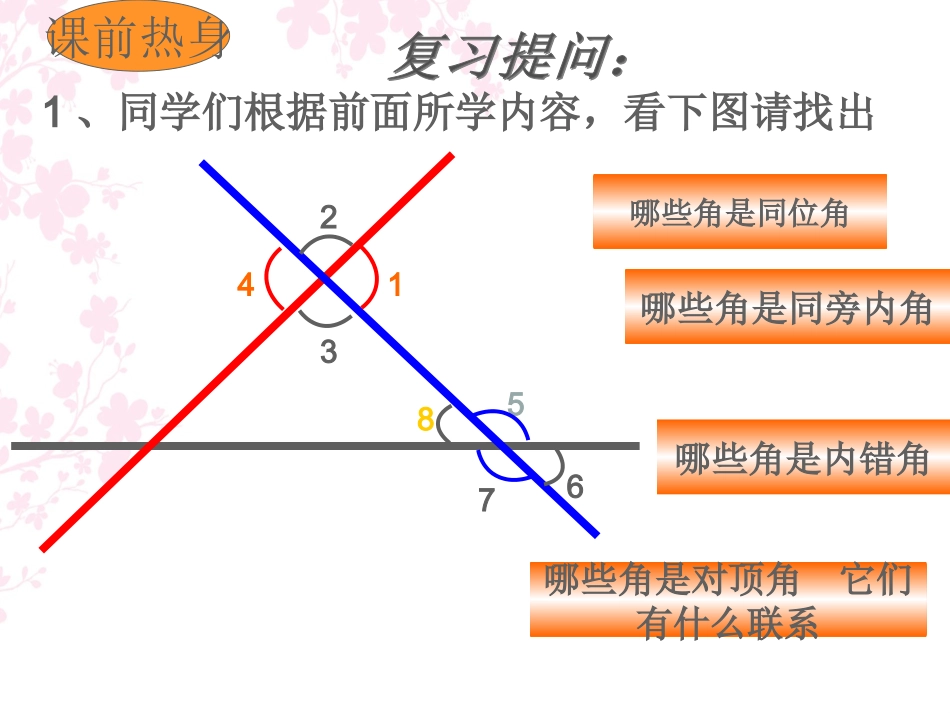
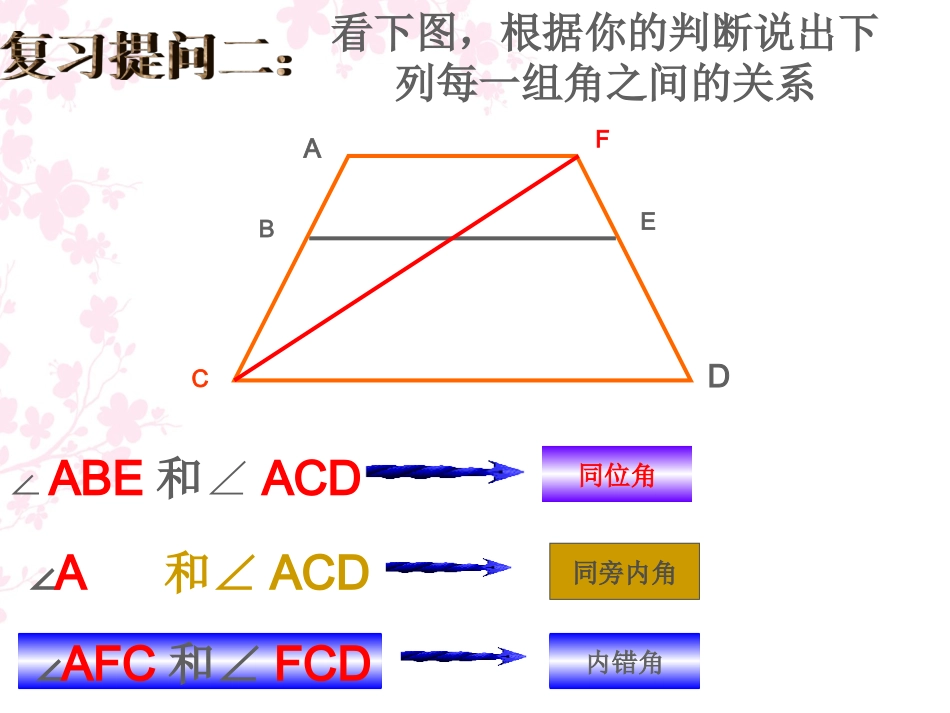
平行线的判定1、同学们根据前面所学内容，看下图请找出哪些角是内错角哪些角是同位角哪些角是同旁内角哪些角是对顶角它们有什么联系23415786课前热身看下图，根据你的判断说出下列每一组角之间的关系∠ABE和∠ACD∠A和∠ACD∠AFC和∠FCDABCFED同位角同旁内角内错角复习提问三：同学们回忆前面所学知识回答问题，在同一平面内，两同学们回忆前面所学知识回答问题，在同一平面内，两条直线之间有条直线之间有几种位置关系几种位置关系呢？呢？一般相交特殊相交两条直线位置关系相交平行判断下列语句是否正确:(1)两条直线不相交,就叫做平行线.()(2)与一条直线平行的直线只有一条.()(3)如果两条直线a、b都和直线c平行，那么直线a、b就平行.()×√×判定两条直线平行的方法有两种：定义：在同一平面内，不相交的两条直线叫平行线。平行公理的推论同学们可以想一想？除应用以上两种方法以外，是否还有其它方法呢？如果两条直线同平行于一条直线，那么两条直线平行。如图，三根木条相交成如图，三根木条相交成∠∠11，，∠∠22，固定木条，固定木条bb、、cc，转动木条，转动木条a,a,观察观察∠∠11，，∠∠22满足什么条件时直线满足什么条件时直线aa与与bb平行平行..当∠当∠11＞∠＞∠22时时当∠当∠11＝∠＝∠22时时当∠当∠11＜∠＜∠22时时①①直线直线aa和和bb不平不平行行②②直线直线aa∥∥bb③③直线直线aa和和bb不平不平行行试一试猜一猜试一试猜一猜猜想：两条直线被第三条直线所截，如果同位角相等，那么两直线平行。51。51。86。86。117。117。.αβ2、观察比较，进行猜想：126。107。168。126。验证猜想：“会不会有某一特定时刻，即使同位角不等而两直线平行呢？”.141。135。72。3、验证猜想：（揭示公理）两条直线被第三条直线所截，如果同位角相等，那么这两条直线平行。简单说成：同位角相等、两直线平行判定两条直线平行的公理：3、验证猜想：（揭示公理）αβabc推理过程: ∠α=∠β(已知)∴ab(∥同位角相等、两直线平行)一般地,判断两直线平行有下面的方法:两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.简单地说,同位角相等同位角相等,,两直线平行两直线平行.4123ABCEFD5HG如图,哪两个角相等能判定直线ABCD?∥如果,能判定哪两条直线平行?∠1=2∠∠3=4∠ABCD∥EFGH∥1432ADCB∠3=4∠∠2=5∠EFGH∥如图，已知∠1+2∠＝180º，AB与CD平行吗？为什么？ABCDEF123例2已知：如图，ABC、CDE都是直线，且∠1=∠2，∠1=∠C，求证：AC∥FD. ∠1=2∠，∠1=C∠（已知）∴∠2=C∠（等量代换）∴ACFD∥（同位角相等，两直线平行）FEBCDA21证明：如图，已知∠1=2∠，AB与CD平行吗？为什么？ABCDEF123一般地,判断两直线平行有下面的方法:两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行.简单地说,内错角相等内错角相等,,两直线平行两直线平行.4123ABCEFD5HG如图,哪两个角相等能判定直线ABCD?∥如果,能判定哪两条直线平行?∠3=2∠∠3=4∠或∠1=4∠ABCD∥ABCD∥1432ADCB∠5=6∠∠4=5∠EFGH∥6例4已知：如图，∠DAB被AC平分，且∠1=∠3，ABCD123求证：AB∥CD. ∠DAB被AC平分（已知）∴∠1=2∠（角平分线定义） ∠1=3∠（已知）∴∠2=3∠（等量代换）∴ABCD(∥内错角相等，两直线平行)证明：如图，已知∠1+2∠＝180º，AB与CD平行吗？为什么？ABCDEF12一般地,判断两直线平行有下面的方法:两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行.简单地说,同旁内角互补同旁内角互补,,两直线平行两直线平行.abl312,ab1.如图,直线被直线所截.(1)若,则与平行吗?根据什么?(2)若,则与平行吗?根据什么?00175,27500275,3105baabl在同一平面内,如果两条直线都垂直于同一条直线，那么这两条直线平行吗？为什么？abc12 b⊥a∴∠2=90°(垂直的定义)∴b∥c.(同位角相等，两直线平行)∴∠1=90°(垂直的定义) c⊥a∴∠1=∠2想一想判定两直线平行有哪些方法？理由：平行理由：如图， ba,ca(⊥⊥已知)∴∠1=2=90°(∠垂直定义)∴bc(∥内错角相等，两直线平行)abc12方法2:理由：如图， ba,ca(⊥⊥已知)∴∠1=2=90°(∠垂直定义)∴∠1+2=180°...