导数的几何意义PPTVIP免费

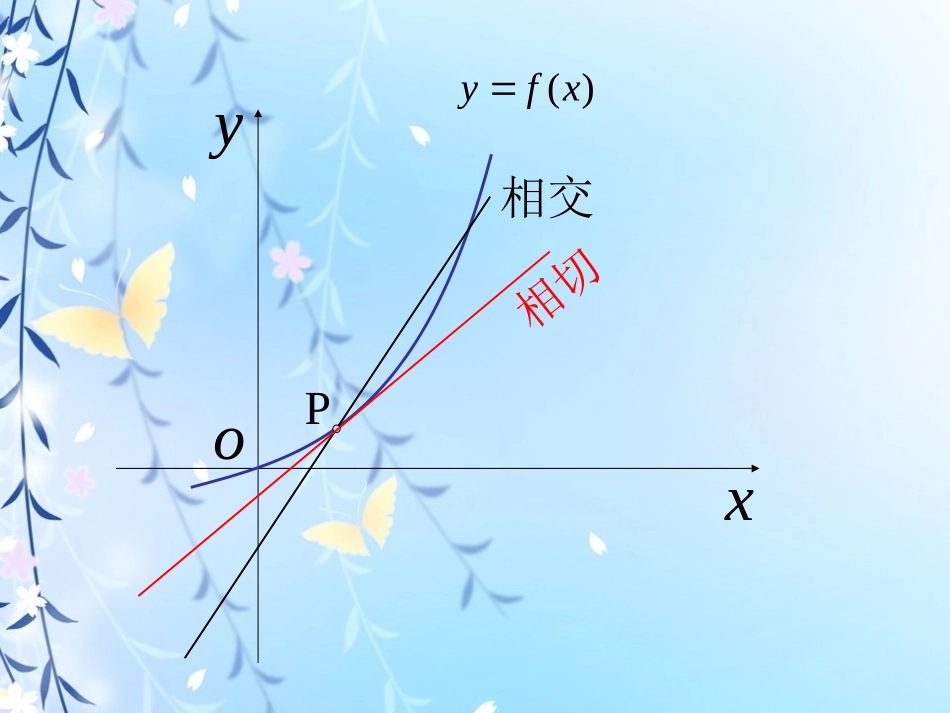
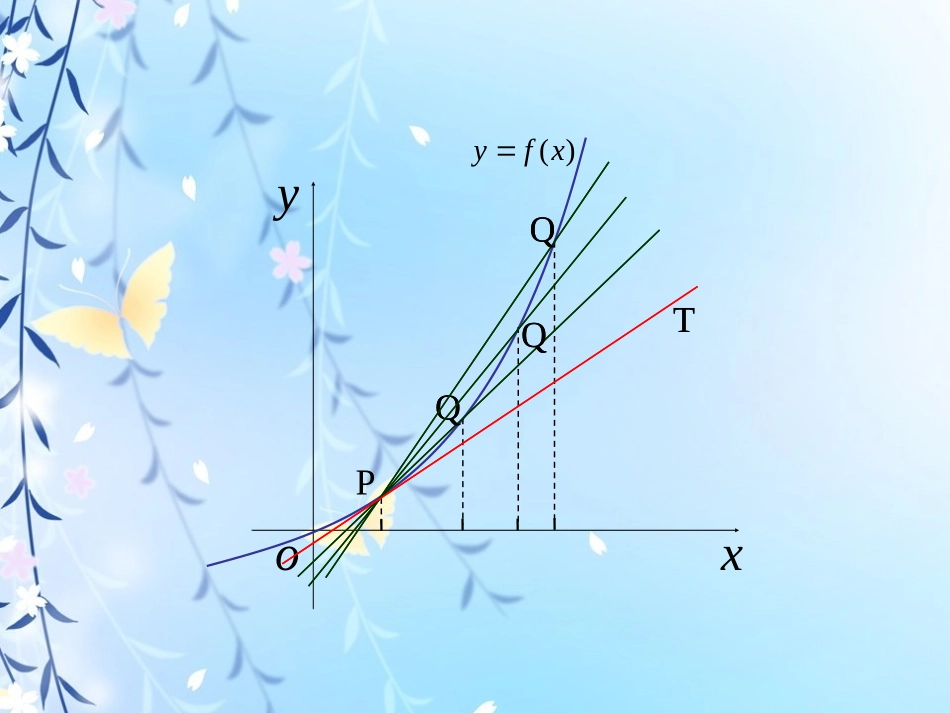
yxo)(xfyP相切相交yxoQPQQ)(xfyT直线PQ的斜率为xyxxxyyyxxyykPQPQPQ0000)()(PQ无限靠近切线PTxykkxPQxPT00limlim相应的,y=f(x)在点P(x0,f(x0))处的切线方程为：函数y=f(x)在点x0处的导数的几何意义,就是000xxxfyy曲线y=f(x)在点P(x0,f(x0))处的切线的斜率．例1、如图，它表示跳水运动中高度随时间变化的函数h(t)=-4.9t2+6.5t+10的图象。根据图象，请描述、比较曲线h(t)在t0,t1,t2附近的变化情况。htol2l0t4t3t2t0t1l1htol2l0t4t3t2t0t1l1解：我们用曲线h(t)在t0,t1,t2处的切线，刻画曲线h(t)在上述三个时刻附近的变化情况。(1)当t=t0时,曲线h(t)在t0处的切线l0平行于x轴.所以,在t=t0附近曲线比较平坦,几乎没有下降.(2)当t=t1时,曲线h(t)在t1处的切线l1的斜率h′(t1)<0.所以,在t=t1附近曲线下降,即函数h(t)在t=t1附近单调递减.(3)当t=t2时,曲线h(t)在t2处的切线l2的斜率h′(t2)<0.所以,在t=t2附近曲线下降,即函数h(t)在t=t2附近也单调递减.与t2相比,曲线在t1附近下降得缓慢些.例2、如图，它表示人体血管中药物浓度c=f(t)(单位：mg/mL)随时间t(单位：min)变化的函数图象。根据图象，估计t=0.5,0.8时，血管中药物浓度的瞬时变化率(精确到0.1)00.20.10.40.60.51.10.70.31.00.90.80.20.10.40.60.51.10.70.31.00.90.8t(min)c(mg/mL)解：血管中某一时刻药物浓度的瞬时变化率，就是药物浓度f(t)在此时刻的导数。作t=0.5处的切线,它的斜率约为00)5.0(f所以,作t=0.8处的切线,它的斜率约为-1.55.1)8.0(f所以,因此在t=0.5和0.8处药物浓度的瞬时变化率分别为0和-1.5.求函数y=f(x)在点x0处的导数的方法是：00xfxxfyxxfxxfxy00xyxfx00lim(2)求平均变化率(3)取极限,得导数(1)求函数的增量例3、某物体的运动方程为s(t)=5t2（位移单位：m，时间单位：s）求它在t＝2s时的速度.解:因为22252025)2(5tttstts520从而20)520(limlim)2(00ttsstt所以例4、已知曲线上一点求：点P处的切线的斜率；点P处的的切线方程．331xy38,2P解:点P处的切线的斜率即在x=2处的导数.331xy323124xxx33231)2(31xf因为23124xxxf从而4)3124(limlim)2(200xxxffxx所以点P处的的切线方程点P处的切线的斜率是4.)2(438xy3164xy即直线练习1、求曲线在点M(3,3)处的切线的斜率及倾斜角．xy9斜率为-1,倾斜角为135°练习2、判断曲线在（1，-）处是否有切线，如果有，求出切线的方程.221xy12切线的方程为21xy注:学了导数的运算后,此类题有更简单的解法.处的导数在是求函数00)()(xxxfyxf如果将x0改为x,则求得的是)(xfy被称为函数y=f(x)的导函数.)(xfy如果函数y=f(x)在开区间(a,b)内的每点处都有导数，此时对于每一个x∈(a,b)，都对应着一个确定的导数，从而构成了一个新的函数。称这个函数为函数y=f(x)在开区间内的导函数，简称导数，也可记作，即)(/xf)(/xf)(/xf/y)(/xf/y＝xxfxxfxyxx)()(limlim00＝小结:相应的,y=f(x)在点P(x0,f(x0))处的切线方程为：函数y=f(x)在点x0处的导数的几何意义,就是000xxxfyy曲线y=f(x)在点P(x0,f(x0))处的切线的斜率．