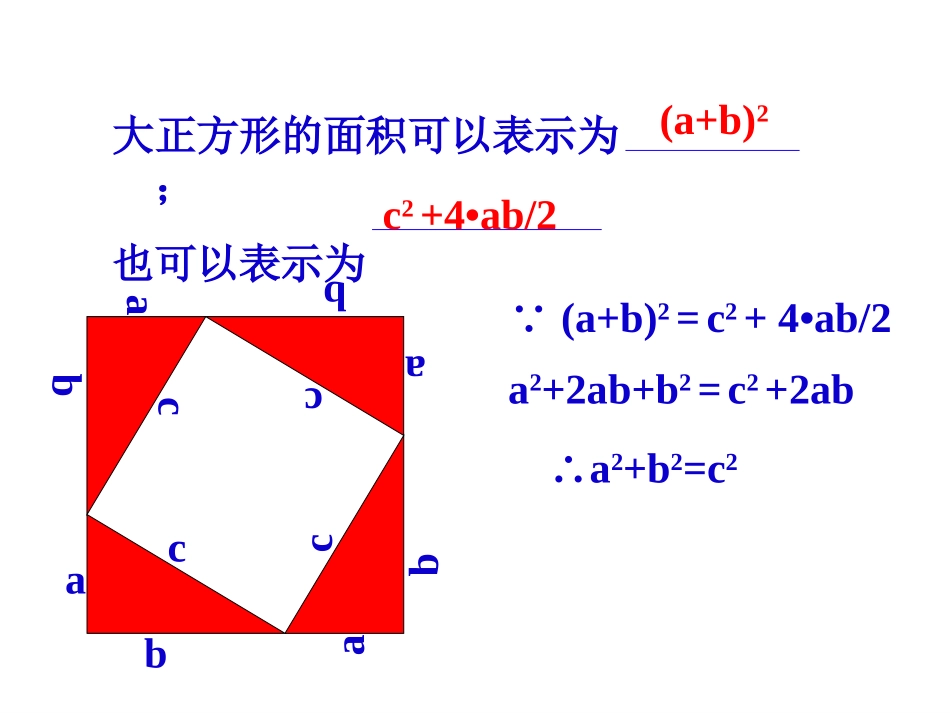
1.2直角三角形22222122122121221221212122212212221211)2())((cbacababbasscabcababsabbababababasbacbaccabcabcabcab (a+b)2=c2+4•ab/2a2+2ab+b2=c2+2ab∴a2+b2=c2大正方形的面积可以表示为;也可以表示为(a+b)2c2+4•ab/2cacacbca c2=4•ab/2+(b-a)2c2=2ab+b2-2ab+a2c2=a2+b2∴a2+b2=c2大正方形的面积可以表示为;也可以表示为c24•ab/2+(b-a)2四年一度的国际数学家大会于2002年8月20日在北京召开,大会会标如图,它是由四个相同的直角三角形与中间的小正方形拼成的一个大正方形.学习目标1定理:斜边和一条直角边对应相等的两个直角三角形全等定理:直角三角形两条直角边的平方和等于斜边的平方。定理:如果一个三角形两边的平方和等于第三边的平方,那么这个三角形是直角三角形。判断下列命题的真假,并说明理由:两个锐角对应相等的两个直角三角形全等;斜边及一个锐角对应相等的两个直角三角形全等;两直角边对应相等的两个直角三角形全等;开启智慧一条直角边和另一条直角边上的中线对应相等的两个直角三角形全等.设矩形的对角线AC与BD的交点为O,那么BO是直角△ABC中一条怎样的特殊线段?它与AC有什么大小关系?ABCDOABCO定理直角三角形斜边上的中线等于斜边的一半 ∠ABC=90°,OA=OC∴AC=2OB或OA=OB=OC学习目标2特殊的直角三角形的性质:1.在直角三角形中,如果有一个锐角等于300,那么它所对的直角边等于斜边的一半.2.在直角三角形中,如果一条直角边等于斜边的一半,那么它所对的锐角等于300.学习目标3互逆命题,逆命题互逆定理,逆定理如果两个角是对顶角,那么这两个角相等。如果两个角相等,那么这两个角是对顶角。三角形中相等的边所对的角相等。三角形中相等的角所对的边相等。直角三角形两条直角边的平方和等于斜边的平方。如果一个三角形两边的平方和等于第三边的平方,那么这个三角形是直角三角形。勾股定理:勾股定理逆定理:学习目标4ACBD300特殊图形:CBADE32你能求出AD和AB吗?CBADE探索1:BC、CD、AB之间的关系?探索2:CD与AD关系?┏┏学习目标5从前有一天,一个醉汉拿着竹竿进屋,横拿竖拿都进不去,横着比门框宽4尺,竖着比门框高2尺。另一个醉汉教他沿着门的两个对角斜着拿竿,这个醉汉一试,不多不少刚好进去了。你知道竹竿有多长吗?请根据这一问题列出方程。(只列不解)问题探讨问题探讨22224xxxx尺,得设:竹竿三角形全等的判定公理:三边对应相等的两个三角形全等(SSS).公理:两边及其夹角对应相等的两个三角形全等(SAS).公理:两角及其夹边对应相等的两个三角形全等(ASA).推论:两角及其中一角的对边对应相等的两个三角形全等(AAS).回顾回顾&&思思考考11想一想:两边及其中一边的对角对应相等的两个三角形全等吗?两边及其中一边的对角对应相等的两个三角形不一定全等.如果其中一边所对的角是直角呢?如果其中一边所对的角是直角,那么这两个三角形全等.请你如何证明你的结论.命题的证明我能行11命题:两边及其中一边的对角对应相等的两个三角形不一定全等.老师提示:举反例证明假命题千万不可忘记噢!证明:这是一个假命题,只要举一个反例即可.如图:ABCA′B′C′A′B′C′●●●(1)(2)(3)由图(1)和图(2)可知,这两个三角形全等;由图(1)和图(3)可知,这两个三角形不全等;因此,两边及其中一边的对角对应相等的两个三角形不一定全等.命题的证明我能行22驶向胜利的彼岸两边及其中一边的对角对应相等的两个三角形不一定全等.但如果其中一边所对的角是直角,那么这两个三角形全等.老师期望:你能写出它的证明过程吗?你能根据上面的证明用文字写出一个定理吗?已知:如图,在△ABC和△A′B′C′中,AC=A′C′,AB=A′B′,C=∠C′=90∠0.求证:△ABC≌△A′B′C′.BACB′A′C′分析:要证明△ABC≌△A′B′C′,只要能满足公理(SSS),(SAS),(ASA)和推论(AAS)中的一个即可.由已知和根据勾股定理易知,第三条边也对应相等.驶向胜利的彼岸直角三角形全等的判定定理及其三种语言我能行33定理:斜边和一条直角边对应相等的两个直角三角形全等(斜边、直角边或HL).如图,在△ABC和△A′...