工程流体力学第4章_流体在圆管中的流动VIP免费

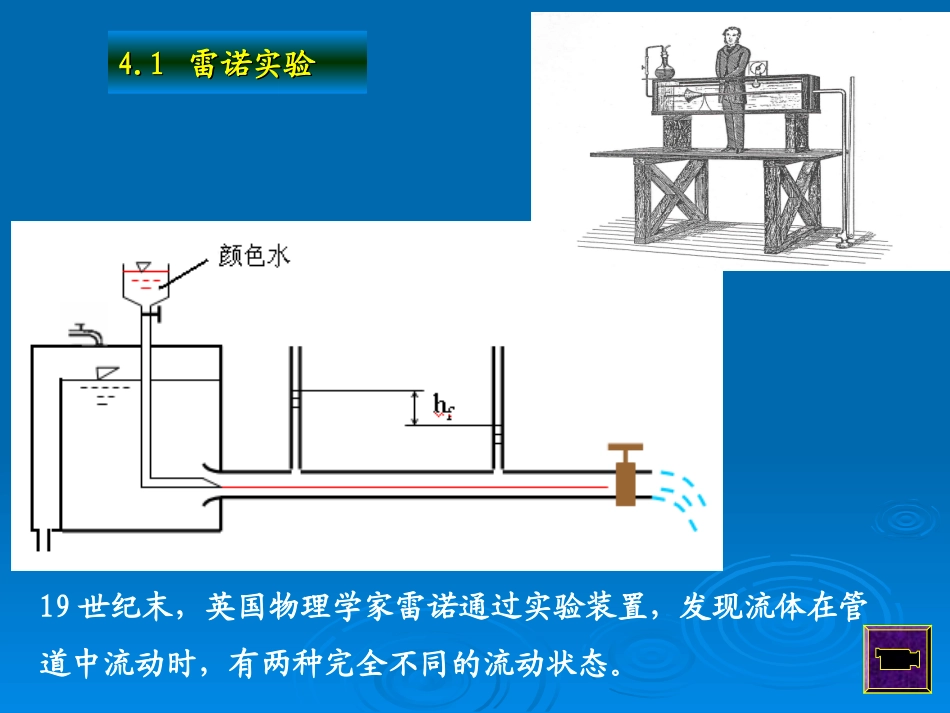
第4章流体在圆管中的流动1.流体在固体内部的管中流动和缝隙中流动;2.流体在固体外部的绕流;3.流体在固体一侧的明渠流动;4.流体与固体不相接触的孔口出流和射流。流体运动按与物体的接触情况分类：在机械工程方面，涉及最多的就是流体在管路中流动，如机床的润滑系统、汽车发动机的冷却系统，车间的供水、供风、供油及通风除尘设备等。4.14.1雷诺实验雷诺实验19世纪末，英国物理学家雷诺通过实验装置，发现流体在管道中流动时，有两种完全不同的流动状态。流速很小时，管内液体沿轴向流动，层与层之间、流束之间不互相混杂，流体质点之间没有径向的运动交换，都保持各自的流线运动，这种流动状态称为层流。流速增大时，颜色水看是动荡，但仍保持完整形状，管内液体仍为层流状态，当到达到某一值时，颜色线开始抖动、分散。这是一种由层流到湍流的过渡状态。kv当流速达到一定值时，质点运动曾现一种紊乱状态，质点流动杂乱无章，说明管中质点流动不仅仅在轴向，在径向也有不规则的脉动现象，各质点大量交换混杂，这种流动状态称为湍流或紊流。4.1.1层流和湍流颜色水颜色水颜色水1.临界速度流体流动速度不断加大，由层流状态开始变成紊流状态的速度称为上临界数（（Vk´Vk´）。）。··流体流动速度不断减小，由紊流状态开始变成层流状态的速度称为下临界数（（VkVk）。）。实验测得实验测得Vk>Vk´Vk>Vk´能否用速度界定流体的流动状态？？？1.层流是一种不稳定的流动状态。4.1.2流动状态的判定用不同的流体在相同直径的管道中进行实验，所测得的临界速度各不相同。kkVV和用同一种流体在不同直径的管道中进行实验，所测得的临界速度也不相同。kkVV和流体的流动状态与管径有关。流体的流动状态与流体物理属性有关、雷诺实验2、雷诺数VlVdVdReRe>13800时，管中流动状态是紊流；Re<2320时，管中流动状态是层流。雷诺实验工程中判断标准：Re<2000，层流；Re>2000，紊流。：特征尺寸l4.14水力直径的概念水力直径大，说明流体与管壁接触少，阻力小，通流能力大，即使通流截面小也不堵塞。一般圆形管道的水力直径比其它通流截面积相同而形状的不同的水力直径大。湿周。管道过流断面面积；其中：SASAdk4水力直径：湿周：是过流断面上流体与固体接触的周长。水力直径是一个直接影响流体在管道中的通流能力的物理量。4.1.3沿程损失与速度的关系1沿程损失沿流程的摩擦阻力，叫作沿程阻力，由此产生的能量损失称为沿程损失。2沿程损失与速度的关系mVKhVKh2211紊流：层流：m=1.75~2在试验管的两侧安装测压管列1、2两断面的伯努利方程：21212211221222fpvpvzzhggggfhgpgpp21表明测压管液柱高度差为其沿程损失水头。改变速度改变速度,,逐次测量层流、湍流两种情况逐次测量层流、湍流两种情况下的与对应的值。将实验结果标在对数坐下的与对应的值。将实验结果标在对数坐标纸上如图标纸上如图4.44.4所示。因此可得所示。因此可得::1.层流:vkvkhf101lglg45tanlglgvkhf11层流的损失规律2.紊流：mfvkvkh22lglgtanlglg)2~75.1(22mvkhmf紊流的损失规律雷诺实验贡献1、揭示了流体流动存在两种状态——层流、紊流（湍流）；2、找出了判定层流、紊流（湍流）的方法----雷诺数Re；VlVdVdRe3、给出了层流、紊流（湍流）的不同损失规律。mVKhVKh2211紊流：层流：m=1.75~24.2圆管中的层流流动层流流动假设：1）研究对象为不可压缩流体；2）一般情况下，流体质点的运动惯性力和质量力忽略不计；3）流体的粘度不变。颜色水4.2.1管中层流流速分布和流量4.2.1管中层流流速分布和流量管中流动流线是平行的，流速以管轴为对称轴，在同一半径上速度相等，流体做等速运动。管中层流运动分析：u，即：管轴上投影为在做匀速运动，所有外力流体对于层流流动，该筒状，则半径为，，长度为设壁厚为取筒状流体为分离体，0:rldr0sin2))((22)(221grdrlddrrlrlpprdr整理得：，忽略二阶微量，代入注意到：12sinzzl)]()[(2211gpzgpzlgrdrd，代入整理得：又：dr...