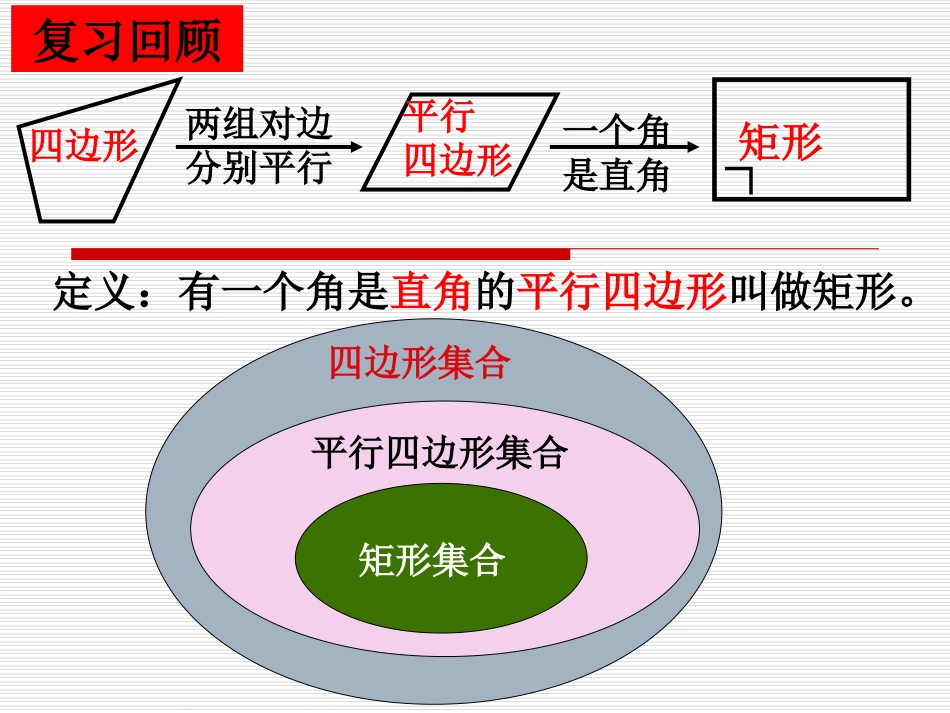
18.2.1矩形的判定掌握矩形的概念和性质。理解并掌握矩形的判定方法。使学生能应用矩形定义、判定等知识,解决简单的证明题和计算题,进一步培养学生的分析能力。教学目标复习回顾四边形平行四边形两组对边分别平行一个角是直角∟矩形四边形集合平行四边形集合矩形集合定义:有一个角是直角的平行四边形叫做矩形。矩形的性质知识要点知识要点ABCD矩形的对边平行且相等。角对角线边矩形的对角线相等。矩形的对角线互相平分。矩形的四个角都是直角。矩形的对角相等。对称性矩形是轴对称图形,也是中心对称图形。直角三角形的性质定理:直角三角形斜边上的中线等于斜边的一半。已知:四边形ABCD是矩形1、若已知AB=8㎝,AD=6㎝,则AC=()㎝OB=()㎝2、若已知∠CAB=40°,则∠OCB=()∠OBA=()∠AOB=()∠AOD=()3、若已知AC=10㎝,BC=6㎝,则矩形的周长=()㎝矩形的面积=()㎝24、若已知∠DOC=120°,AD=6㎝,则AC=()㎝ODCBA550°10100°40°12482880°试一试脸蛋方方是矩形,例如黑板和窗门.对角线段皆相等,相互交叉且平分.内有直角三角形,斜边中线半斜边.若要牢记其定义,直角平行四边形.矩形之歌怎样判定一个四边形是否为矩形?根据矩形的定义去判定.有一个角是直角的平行四边形是矩形.导入新课导入新课猜想1:猜想2:ABCD除了根据定义判定,还有其它判定矩形的方法吗?自学指导自学指导工人师傅为了检验两组对边相等的四边形窗框是否成矩形,一种方法是量一量这个四边形的两条对角线长度,如果对角线长度相等,则窗框一定是矩形,你知道为什么吗?猜想1:对角线相等的平行四边形是矩形.自学指导自学指导已知:平行四边形ABCD,AC=BD。求证:平行四边形ABCD是矩形。证明:∵AB=CD,BC=BC,AC=BD∴△ABC△DCB△(SSS)∵AB//CD∴∠ABC+DCB=180°∠∴∠ABC=DCB=90°∠又∵四边形ABCD是平行四边形∴四边形ABCD是矩形∴∠ABC=DCB∠ADCBO定理证明定理证明自学指导自学指导对角线相等的平行四边形是矩形艾力同学用画“边——直角、边——直角、边——直角、边”这样四步,画出了一个四边形,他说这就是一个矩形,他的判断对吗?为什么?猜想2:有三个角是直角的四边形是矩形。自学指导自学指导有三个角是直角的四边形是矩形。已知:四边形ABCD,∠A=B=C=90°∠∠求证:四边形ABCD是矩形.定理证明定理证明证明:由多边形内角和公式(n-2)·180得,四边形内角和=(4-2)180=360°∴∠D=360°-90°-90°-90°=90°∵∠A+∠B=180°ADBC∴∥∵∠B+∠C=180°ABCD∴∥∴四边形ABCD是平行四边形。又∵∠A=90°∴四边形ABCD是矩形。BADC自学指导自学指导有一个角是直角的平行四边形是矩形。对角线相等的平行四边形是矩形。对角线相等且互相平分的四边形是矩形。有三个角是直角的四边形是矩形。矩形的判定定理知识要点知识要点矩形的定义:有一个角是直角的平行四边形。矩形的性质:矩形的判定:具有平行四边形的一切特征。四个角都是直角。对角线相等且平分。有一个角是直角的平行四边形。对角线相等的平行四边形。有三个角是直角的四边形。对角线相等且平分的四边形。课堂小结通过这节课的学习,你有什么收获?随堂练习1.下列判定矩形的说法是否正确?(1)对角线相等的四边形是矩形。(2)对角线互相平分且相等的四边形是矩形。(3)有一个角是直角的四边形是矩形。(4)有三个角都相等的四边形是矩形。(√)(×)(×)(×)(5)有三个角是直角的四边形是矩形。(√)(6)四个角都相等的四边形是矩形。(7)对角线相等,且有一个角是直角的四边形是矩形。(10)一组邻边垂直,一组对边平行且相等的四边形是矩形。(9)对角线相等且互相垂直的四边形是矩形。(8)一组对角互补的平行四边形是矩形。(√)(×)(√)(√)(×)随堂练习2.下列说法错误的是()A.矩形的对角线互相平分。B.矩形的对角线相等。C.有一个角是直角的四边形是矩形。D.有一个角是直角的平行四边形叫做矩形。3.矩形的对角线把矩形分成的三角形中全等三角形一共有()A.2对B.4对C.6对D.8对CB随堂练习4.四个学生正在做投圈游戏,他们分别站在一个矩形的四个顶点处,目标物放在对角线的交点处,这样的队形对每个人公平吗?为什么?OABCD公平,因为OA=OC=OB=OD随堂练习课后作业1、教材:习题18.2第8,9题。2、练习册对应部分习题。