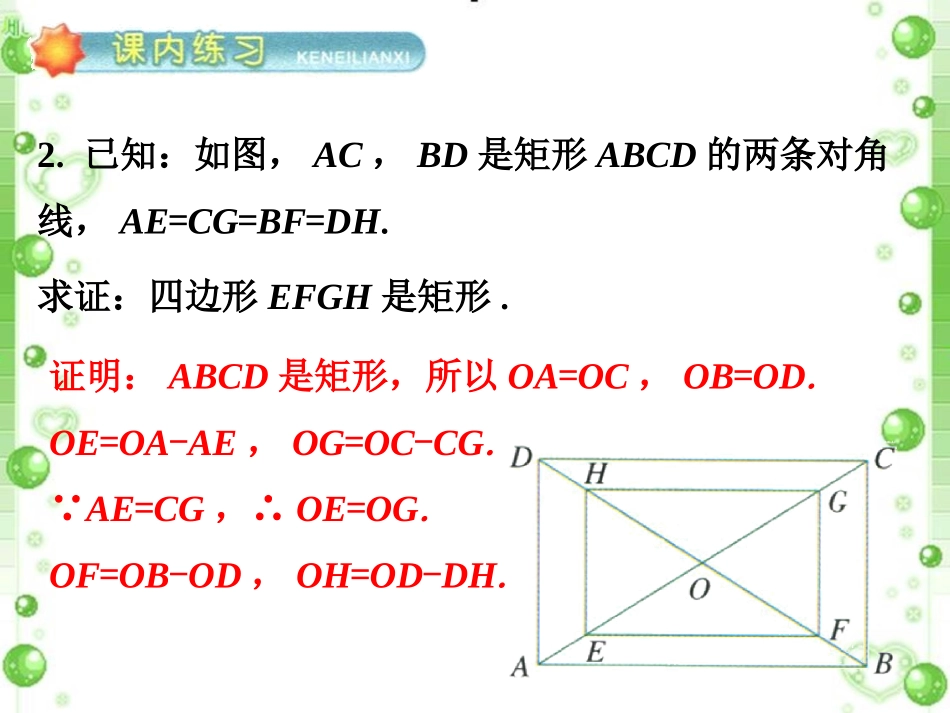
1.判断下列命题是否正确,并说明理由.(1)对角互补的平行四边形是矩形.(2)一组邻角相等的平行四边形是矩形.(3)对角线相等的四边形是矩形.(4)内角相等的四边形是矩形.(1)正确,平行四边形对角相等,对角若互补,只能都是90°.(2)正确,平行四边形邻角互补,邻角若相等,只能都是90°.(3)错误,对角线相等且平分的四边形是矩形.(4)正确,四边形内角和为360°,都相等,都为90°.2.已知:如图,AC,BD是矩形ABCD的两条对角线,AE=CG=BF=DH.求证:四边形EFGH是矩形.证明:ABCD是矩形,所以OA=OC,OB=OD.OE=OA-AE,OG=OC-CG.∵AE=CG,∴OE=OG.OF=OB-OD,OH=OD-DH.∵BF=DH,∴OF=OH.四边形EFGH对角线互相平分,所以是平行四边形.因为ABCD是矩形,所以AC=BD.EG=AC-AE-CG.FH=BD-BF-DH.所以EG=FH.平行四边形EFGH对角线相等,因此是矩形.