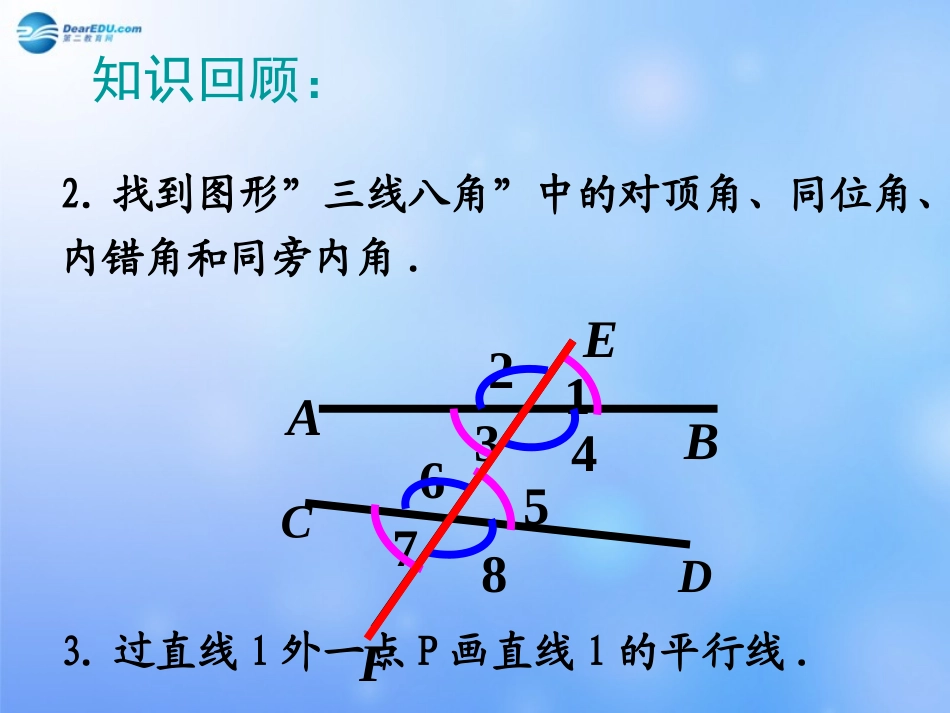
知识回顾:(1)两条不相交的直线叫平行线;(2)过一点画已知直线的平行线能且只能画一条;(3)与已知直线平行的直线有且只有一条;(4)若直线a、b都和c平行,那么a与b平行.1.判断下列语句是否正确,并加以改正。3.过直线l外一点P画直线l的平行线.2.找到图形”三线八角”中的对顶角、同位角、内错角和同旁内角.23417856CAEBDF知识回顾:互动合作,探究新知数学图形的简洁美.平行线的识别平行线的识别1.两条直线被第三条直线所截,如果同位角相等,那么两直线平行。简单地说:同位角相等,两直线平行。abl21∵∠1=∠2()∴a∥b()用法:已知同位角相等,两直线平行平行线的识别平行线的识别思考?思考?abl12①如图:如果∠1=2∠,那么a与b平行吗?②如图:如果∠1+2=180∠o,那么a与b平行吗?abl1233内错角相等,两直线平行。abl12①如图:如果∠1=∠2,那么a与b平行吗?∵∠1=∠2平行线的识别平行线的识别(已知)(内错角相等,两直线平行)用法:∴a∥b②如图:如果∠1+2=180∠o,那么a与b平行吗?abl12同旁内角互补,两直线平行。∵____+____=180o(已知)∴___∥___(同旁内角互补,两直线平行)∠1∠2ab平行线的识别平行线的识别进一步探索!进一步探索!①∵∠2=___(已知)∴___∥___②∵∠3=5∠(已知)∴___∥___③∵∠4+___=180o(已知)∴___∥___∠6ABCDABCD∠5ABCDAC14235867BD1.如图:平行线的识别平行线的识别同位角相等,两直线平行内错角相等,两直线平行同旁内角互补,两直线平行①∵∠1=_____(已知)∴ABCE∥②∵∠1+_____=180o(已知)∴CDBF∥③∵∠1+5=180∠o(已知)∴_____∥_____ABCE∠2④∵∠4+_____=180o(已知)∴CEAB∥平行线的识别平行线的识别∠3∠32.如图:13542CFEADB内错角相等,两直线平行同旁内角互补,两直线平行同旁内角互补,两直线平行同旁内角互补,两直线平行如图,∠1=100°,∠2=100°,ab∥吗?若∠2=100°,∠3=___时,ab∥。12ab80°23ab思考?如图,如果∠B=∠1,则可得_______//_______根据是________________________________如果∠D=∠1,则可得到_______//_______根据是____________________________1DCBAADBC同位角相等,两直线平行ABCD内错角相等,两直线平行例1.如图,四边形ABCD中,已知∠B=60°,∠C=120°,AB与CD平行吗?AD与BC平行吗?DCBA解:直线AB与CD平行,∵∠B=60°,∠C=120°∴∠B+C=180°,∴AB//CD(同旁内角互补,两直线平行)根据题目条件无法判定AD与BC平行。例2两条直线垂直于同一条直线,这两条直线平行吗?答:理由:abc12平行∵ba,ca.(⊥⊥已知)如图∵ba,ca.⊥⊥∴∠1=2=90∠o(垂直定义)∴ba(∥同位角相等,两直线平行)•例1如图所示:(1)如果已知∠1=∠3,则可判定____∥____,其理由是________________________;•(2)如果已知∠4+∠5=180°,则可判定____∥____,其理由是__________________________;•(3)如果已知∠1=∠6,则可判定____∥____,其理由是______________________;ABDE同位角相等,两直线平行.同旁内角互补,两直线平行.BCEFABDE内错角相等,两直线平行.•(4)如果已知∠5+∠2=180°,那么根据对顶角相等,有∠2=_____,因此可知∠4+∠5=______,所以可判定____∥____,其理由是_______________________.∠4180°BCEF同旁内角互补,两直线平行.3.某人骑自行车从A地出发,沿正东方向前进至B处后,右转150,沿直线向前行驶到C处(如图).这时他想仍按正东方向?请画出他应怎样调整行驶的路线,并说明理由.150CABDE15°同位角相等内错角相等同旁内角互补两直线平行平行线的识别示意图平行线的识别示意图识别数量关系位置关系