第 3 章 静力学平衡问题VIP免费

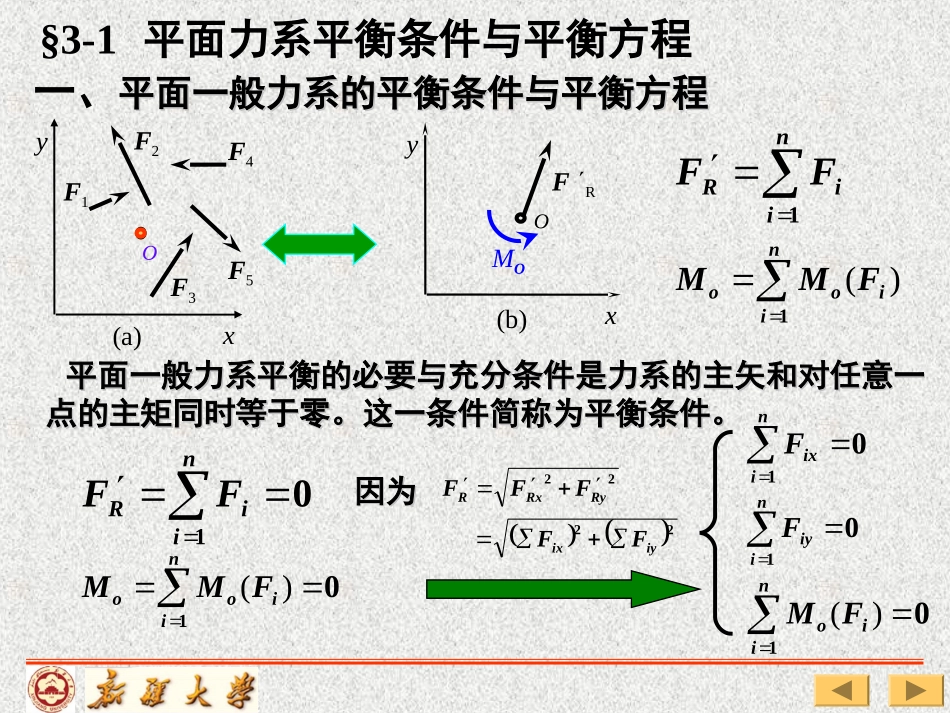
§3-4考虑摩擦时的平衡问题考虑摩擦时的平衡问题§3-3简单的刚体系统平衡问题简单的刚体系统平衡问题§3-2简单的空间力系平衡问题简单的空间力系平衡问题第3章静力学平衡问题§3-1平面力系的平衡条件与平衡方程平面力系的平衡条件与平衡方程平面一般平面一般力系平衡的必要与充分条件是力系的主矢和对任意一力系平衡的必要与充分条件是力系的主矢和对任意一点的主矩同时等于零。这一条件简称为平衡条件。点的主矩同时等于零。这一条件简称为平衡条件。01niiRFF§3-1平面力系平衡条件与平衡方程yx(b)OFRMOxy(a)F4F2F1F5F3OniiooFMM1)(一、平面一般力系的平衡条件与平衡方程平面一般力系的平衡条件与平衡方程01niiooFMM)(01niixF01niiyF01niioFM)(因为因为2222iyixRyRxRFFFFFniiRFF1平面一般力系的平衡方程（基本形式）独立平衡方程只有三个独立平衡方程只有三个01niixF01niiyF01niioFM)(为了书写方便，通常将平面一般力系的平衡方程简写为0xF0)(FMo0yF上述平衡方程表明，平面力系平衡的必要与充分条件是：上述平衡方程表明，平面力系平衡的必要与充分条件是：力系中所有的力在直角坐标系力系中所有的力在直角坐标系OxyOxy的各坐标轴上的投影的的各坐标轴上的投影的代数和以及所有的力对任意点之矩的代数和同时等于零。代数和以及所有的力对任意点之矩的代数和同时等于零。求解力系平衡问题的方法和步骤。（1）选取研究对象；（2）分析研究对象受力，画受力图；（3）根据力系的类型列写平衡方程；选取适当的坐标轴和矩心，以使方程中未知量个数最少；尽可能每个方程中只有一个未知量。（4）求解未知量，分析和讨论计算结果。图示简支梁AB，梁的自重及各处摩擦均不计。试求A和B处的支座约束力。(b)qACBDMe2aa4axyFNBFAxFAy(a)qACBDMe2aa4a解：(1)选AB梁为研究对象。(2)画受力图如右图所示。例题3-1(4)列平衡方程解得eNe0,1,243.24AxBAyFMFqaaMFqaa(b)qACBDMe2aa4axyFNBFAxFAy0xF0AxF0yF02NBAyFaqF0)(FMo042aFMaaqNBe解：以刚架为研究对象，受力如图解：以刚架为研究对象，受力如图。0:0xAxFFqb0:0yAyFFP()0:AMF0212qbPaMA解得：AxFqbAyFP221qbPaMA例1求图示刚架的约束反力求图示刚架的约束反力。APabqAPqFAyFAxMA例题3-2MMAA平面刚架的所有外力的作用线都位于刚架平面内。A处为固定端约束。若图中q、FP、M、l等均为已知，试求试求::A处的约束力。FFAxAxFFAyAyqlll2lM例题3-3解：解：1.选择研究对象。2受力分析,画出受力图如图所示。FPAqlll2lMFPA3.建立平衡方程求解未知力应用平衡方程Fx=0,MA=0，Fy=0,0qlFAxP0AyFFP302AlMMFlql由此解得qlFAxPAyFFFFAxAxFFAyAyMMAAqlll2lMFPAP32AMMFlql2二力矩式（AB不垂直于x轴）二、平面一般力系平衡方程的其它形式二、平面一般力系平衡方程的其它形式0()0()0xABMMFFFxy(b)ABFR=0xy(a)F4F2F1F5F3M()0()0()0ABCMMMFFF三力矩式(A、B、C三点不共线)xy(a)F4F2F1F5F3Mxy(b)ABFRC=0求图示梁的支座反力。求图示梁的支座反力。解：以梁为研究对象，受力如图解：以梁为研究对象，受力如图。0:cos0xAxFFP()0:sin()0ABMFaPabmF解得：解得：cosAxFPsin()BmPabFasinAymPbFaABCPabmABCPmFBFAyFAx例题3-400bPmaFFMAyBsin:)(F5OF4F2F1F3xyxyRFORxFRyF0iRFF因为因为02222yxRyRxRFFFFF0xF0yF平面汇交力系的平衡方程三、平面汇交力系与平面力偶系的平衡方程1.平面汇交力系的平衡方程平面力偶系可以合成为一平面力偶系可以合成为一个合力偶个合力偶,,合力偶之合力偶之矩等于力偶系中各力偶之矩的代数和矩等于力偶系中各力偶之矩的代数和。。MM==MMii2.平面力偶系的平衡方程平面力偶系的平衡方程F1h1F2h2h3F3hF平面力偶系的平衡方程MM==MMii=0=0图示平面刚架的...