勾股定理在折叠问题中的应用VIP免费

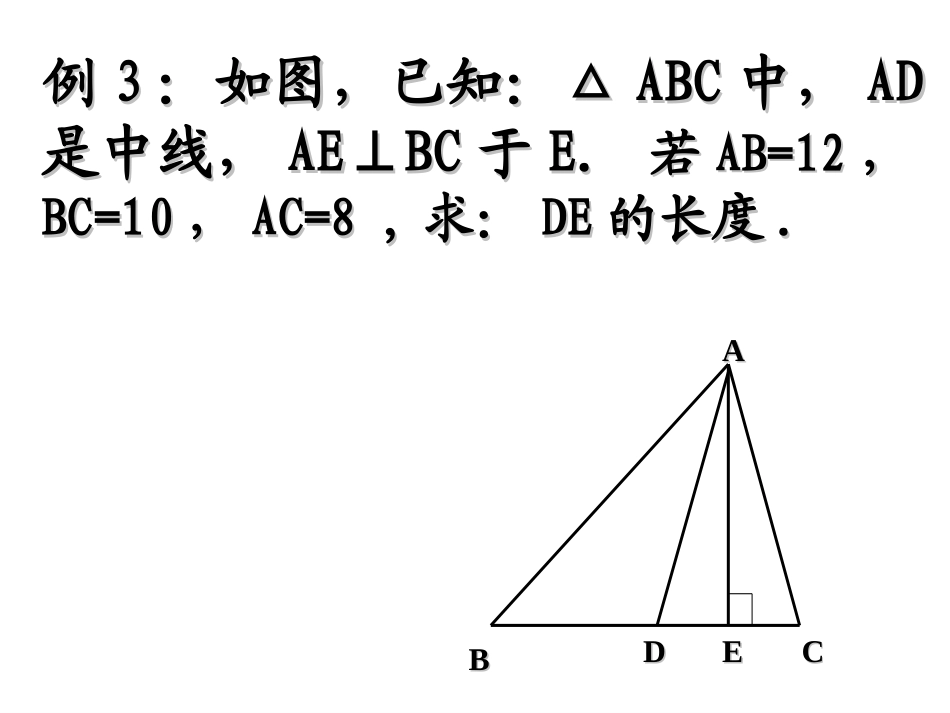
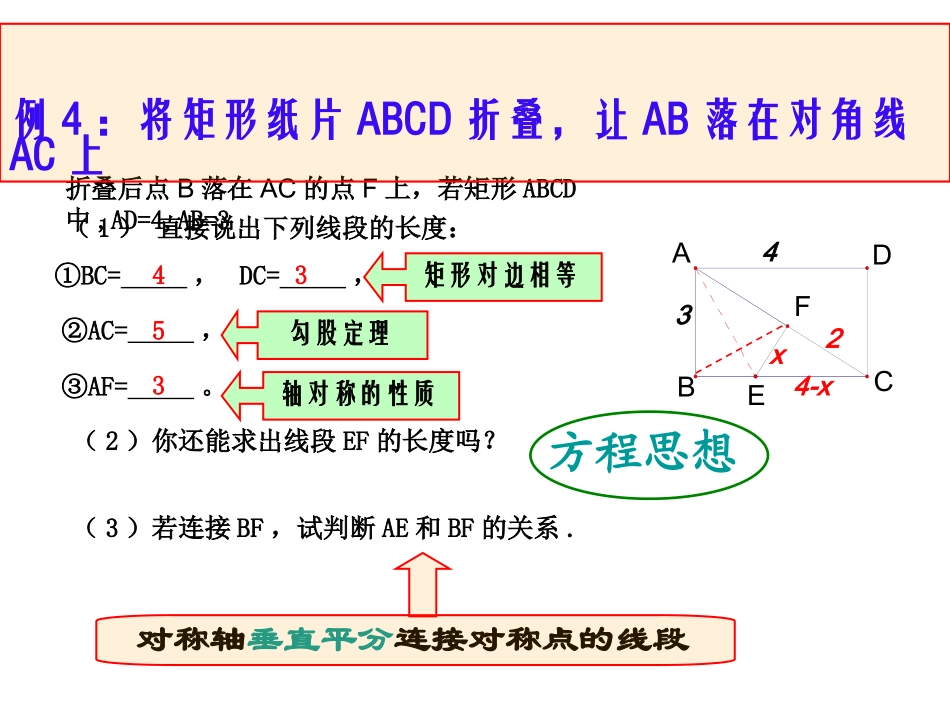
勾股定理在折叠问题中的应用例例33：如图，已知：△：如图，已知：△ABCABC中，中，ADAD是中线，是中线，AE⊥BCAE⊥BC于于E.E.若若AB=12AB=12，，BC=10BC=10，，AC=8,AC=8,求：求：DEDE的长度的长度..AACCEEDDBB折叠后点B落在AC的点F上，若矩形ABCD中,AD=4,AB=3EFDACB（1）直接说出下列线段的长度：43x24-x例4：将矩形纸片ABCD折叠，让AB落在对角线AC上4353（2）你还能求出线段EF的长度吗？②AC=，③AF=。（3）若连接BF，试判断AE和BF的关系.①BC=，DC=，对称轴垂直平分连接对称点的线段矩形对边相等勾股定理轴对称的性质方程思想归纳：说明线段相等的常用方法(1)两三角形全等（对应边相等）(2)同一三角形中等角对等边……..⑴猜想叠合部分是什么图形？验证你的猜想.△AFC为等腰三角形ABCDEFCFDAFECDAEDFCEFARtDE方法一：三角形知方法二：为等腰AFC∴△FAC＝∠ACF∠∴BCA＝∠FAC∠BC∥AD又BCA＝∠ACF∠由折叠例5：将矩形纸片ABCD沿对角线AC折叠⑴猜想叠合部分是什么图形？验证你的猜想.△AFC为等腰三角形⑵若矩形ABCD中AD=4,AB=3,求△AFC的腰长.例5：将矩形纸片ABCD沿对角线AC折叠ABCDEF82582543DFCRt4,222的腰长为即解得：）（中：故则解：设AFCxxxxFDxFCAFxFC求解CDAF21=S利用AFC方法一：直接你会求△AFC的面积吗？DFCADCAFCDFCADCSSSCDDFSCDADS21,21方法二：（2010，青岛）把一张矩形纸片（矩形ABCD）按如图方式折叠，使顶点B和点D重合，折痕为EF.若AB＝3cm，BC＝5cm，则重叠部分△DEF的面积是________cm2.变式：如图,把长方形纸片ABCD折叠,使顶点A与顶点C重合在一起,EF为折痕。若AB=9,BC=3,试求以折痕EF为边长的正方形面积。AD