反比例函数图像和性质(第1课时)课件VIP免费

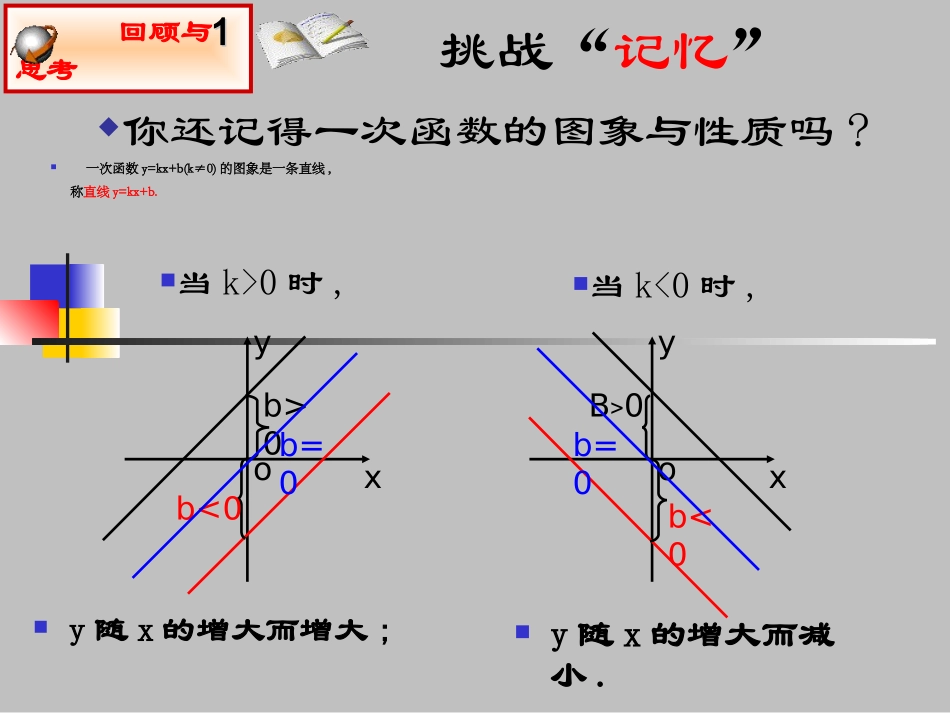
17.1.2反比例函数的图象和性质（1）挑战“记忆”你还记得一次函数的图象与性质吗?回顾与思考11一次函数y=kx+b(k≠0)的图象是一条直线,称直线y=kx+b.y随x的增大而增大;xyoxyoy随x的增大而减小.b<0b>0b=0b<0B>0b=0当k>0时,当k<0时,小练习:1、正比例函数y=2x经过第象限.一、三2、已知矩形面积为6，则它的长y与宽x之间的函数关系式为，y是x的函数.6yx反比例3、函数y=2xm+1是反比例函数，则m=.4、反比例函数经过点（1，）.4yx反比例函数的定义中需要注意什么？1、K是非零常数2、自变量x的次数为-13、自变量x的取值范围x≠0kyx-241、什么是反比例函数？2、反比例函数的定义中还需要注意什么？◆自变量x的取值范围一般地，形如的函数叫做反比例函数．kyx◆自变量x的次数为3、请回忆：正比例函数的图象和性质-2（k是常数，k≠0）-1x≠0◆若函数y=（m-2)xm2-5是反比例函数，则m=，性质图象名称解析式图象位于：一、三象限y随x的增大而增大图象位于：二、四象限y随x的增大而减小K>0K<0y=kx(k≠0)直线(过原点）增减性：增减性：“预见性”,猜一猜反比例函数的图象又会是什么样子呢?你还记得作函数图象的一般步骤吗？给反比例函数“照相”回顾与思考22.0,,,的反比例函数是的形式那么称为常数之间的关系可以表示成如果两个变量一般地xykkxkyyx用图象法表示函数关系时,首先在自变量的取值范围内取一些值,列表,描点,连线(按自变量从小到大的顺序,用一条平滑的曲线连接起来).x画出反比例函数和的函数图象。y=x6y=x6函数图象画法列表描点连线y=x6y=x6描点法注意：①列表时自变量取值要均匀和对称②x≠0③选整数较好计算和描点。例1123456-1-3-2-4-5-61234-1-2-3-40-6-556yxxy=x6y=x6123456-1-3-2-4-5-61234-1-2-3-40-6-556xy16233241.551.2616-1-6-2-3-3-1.5-2-4-5-1.2-6-1…………-663-32-21.5-1.51.2-1.21-1……y=x6y=-x6你认为作反比例函数图象时应注意哪些问题？•列表时,自变量的值可以选取一些互为相反数的值,这样既可简化计算,又便于对称性描点;•列表描点时,要尽量多取一些数值,多描一些点,这样既可以方便连线,又较准确地表达函数的变化趋势;•连线时一定要养成按自变量从小到大的顺序，依次用平滑的曲线连接,从中体会函数的增减性；[注意哟]：图象不会与x轴、y轴相交做一做55“心动”不如行动操作：函数图象画法列表描点连线描点法画出反比例函数和的函数图象。4yx4yx108642-2-4-6-8-15-10-551015gx=-4xfx=4xxy44yx反比例函数的图象和性质反比例函数的图象是由两支双曲线组成的.因此称反比例函数的图象为双曲线;当k>0时,两支双曲线分位于第一,三象限内;当k<0时,两支双曲线分别位于第二,四象限内;１、这几个函数图象有什么共同点？２、函数图象分别位于哪几个象限？３、y随的x变化有怎样的变化？123456-1-3-2-4-5-61234-1-2-3-40-6-556yx123456-1-3-2-4-5-61234-1-2-3-40-6-556xy发现函数值y怎样随着自变量x的变化而变化？·AB·如图xB0K<0当k＞0时，函数图象的两个分支分别在第一、三象限，在每个象限内，y随x的增大而减小.当k＜0时，函数图象的两个分支分别在第二、四象限，在每个象限内，y随x的增大而增大.1.反比例函数的图象是双曲线;2.图象性质见下表：图象性质y=xk反比例函数的图象和性质：学了就用m<23、下列反比例函数图像的一个分支,在第三象限的是()二、四B1、已知反比例函数的函数图象位于第一、三象限，则m的取值范围是.xmy2xyDxkyCxyBxyA3)()(2)(3)(14、函数的图象在第象限.21ayx2、下列函数中，其图象位于第二、四象限的有,在其图象所在的象限内，y随x的减小而增大的有.(1),(4)(2),(3)xyxyxyxy8001)4(43)3(21)2(23)1(...