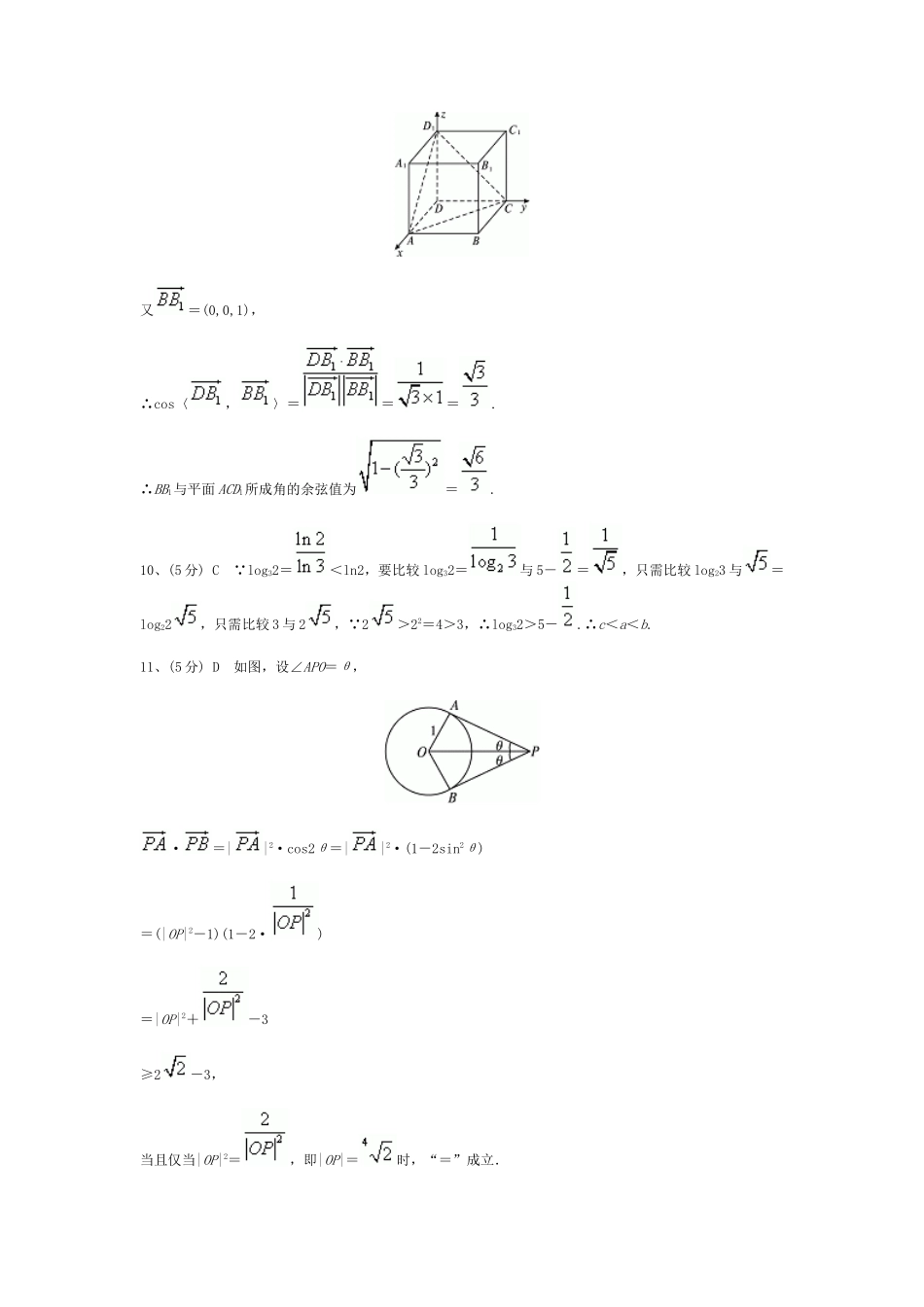
2010年普通高等学校夏季招生考试数学文史类(全国卷Ⅰ)一、选择题(本大题共12题,共计60分)1、(5分)Ccos300°=cos(300°-360°)=cos(-60°)=cos60°=2、(5分)C M={2,3,5},∴N∩(M)={1,3,5}∩{2,3,5}={3,5}.3、(5分)B线性约束条件对应的平面区域如图所示,由z=x-2y得y=-,当直线y=-在y轴上的截距最小时,z取得最大值,由图知,当直线通过点A时,在y轴上的截距最小,由,解得A(1,-1).所以zmax=1-2×(-1)=3.4、(5分)A数列{an}为等比数列,由a1a2a3=5得=5,由a7a8a9=10得=10,所以=50,即(a2a8)3=50,即=50,所以=5(an>0).所以a4a5a6==5.5、(5分)A(1-x)4(1-)3的展开式中x2项为(-x)1·(-)2+(-x)2=-6x2,其系数为-6.6、(5分)C不妨设AB=AC=AA1=1,建立空间直角坐标系如图所示,则B(0,-1,0),A1(0,0,1),A(0,0,0),C1(-1,0,1),∴=(0,1,1),=(-1,0,1).∴cos〈,〉===∴〈,〉=60°.∴异面直线BA1与AC1所成的角为60°.7、(5分)C函数f(x)=|lgx|的图象如图所示,由图象知a,b一个大于1,一个小于1,不妨设a>1,0<b<1. f(a)=f(b),∴f(a)=|lga|=lga=f(b)=|lgb|=-lgb=lg.∴a=.∴a+b=b+>2=2.8、(5分)B在△PF1F2中,|F1F2|2=|PF1|2+|PF2|2-2|PF1|·|PF2|·cos60°=(|PF1|-|PF2|)2+|PF1|·|PF2|,即(2)2=22+|PF1|·|PF2|,解得|PF1|·|PF2|=4.9、(5分)D不妨设正方体的棱长为1,如图建立空间直角坐标系,则D(0,0,0),B(1,1,0),B1(1,1,1).平面ACD1的法向量为=(1,1,1),又=(0,0,1),∴cos〈,〉===.∴BB1与平面ACD1所成角的余弦值为=.10、(5分)C log32=<ln2,要比较log32=与5-=,只需比较log23与=log22,只需比较3与2, 2>22=4>3,∴log32>5-.∴c<a<b.11、(5分)D如图,设∠APO=θ,·=||2·cos2θ=||2·(1-2sin2θ)=(|OP|2-1)(1-2·)=|OP|2+-3≥2-3,当且仅当|OP|2=,即|OP|=时,“=”成立.12、(5分)B不妨取AB⊥CD,过CD作平面PCD,使AB⊥平面PCD,交AB于P.设点P到CD的距离为h,则有V四面体ABCD=×2××2×h=h.当直径通过AB与CD的中点时,hmax=2=2.故Vmax=二、填空题(本大题共4题,共计20分)1、(5分){x|-2<x<-1,或x>2}解析:不等式>0可化为(x-2)(x2+3x+2)>0,即(x-2)(x+1)(x+2)>0,解得-2<x<-1,或x>2.∴原不等式的解集为{x|-2<x<-1,或x>2}.2、(5分)-解析: α为第二象限角,sinα=,∴cosα=-.∴tanα==-.∴tan2α===-.3、(5分)30解析:分两类:①选A类选修课2门,B类选修课1门,有·=12(种);②选A类选修课1门,B类选修课2门,有C·C=3×6=18(种).共有12+18=30(种).4、(5分)解析:如图,设椭圆的标准方程为+=1(a>b>0)不妨设B为上顶点,F为右焦点,设D(x,y).由=2,得(c,-b)=2(x-c,y),即,解得,D(,-).由D在椭圆上得:=1,∴=,∴e==.三、解答题(本大题共6题,共计70分)1、(10分)解:设数列{an}的公差为d.依题设有即解得a1=1,d=3或a1=8,d=-4.因此Sn=n(3n-1)或Sn=2n(5-n).2、(12分)解:由a+b=acotA+bcotB及正弦定理得sinA+sinB=cosA+cosB,sinA-cosA=cosB-sinB,从而sinAcos-cosAsin=cosBsin-sinBcos,sin(A-)=sin(-B).又0<A+B<π,故A-=-B,A+B=.所以C=.3、(12分)解:(1)记A表示事件:稿件能通过两位初审专家的评审;B表示事件:稿件恰能通过一位初审专家的评审;C表示事件:稿件能通过复审专家的评审;D表示事件:稿件被录用.则D=A+B·C,P(A)=0.5×0.5=0.25,P(B)=2×0.5×0.5=0.5,P(C)=0.3,P(D)=P(A+B·C)=P(A)+P(B·C)=P(A)+P(B)·P(C)=0.25+0.5×0.3=0.40.(2)记A0表示事件:4篇稿件中没有1篇被录用;A1表示事件:4篇稿件中恰有1篇被录用;A2表示事件:4篇稿件中至少有2篇被录用.=A0+A1.P(A0)=(1-0.4)4=0.1296,P(A1)=×0.4×(1-0.4)3=0.3456,P()=P(A0+A1)=P(A0)+P(A1)=0.1296+0.3456=0.4752,P(A2)=1-P()=1-0.4752=0.5248.4、(12分)解法一:(1)连结BD,取DC的中点G,连结BG,由此知DG=GC=BG=1,即△DBC...