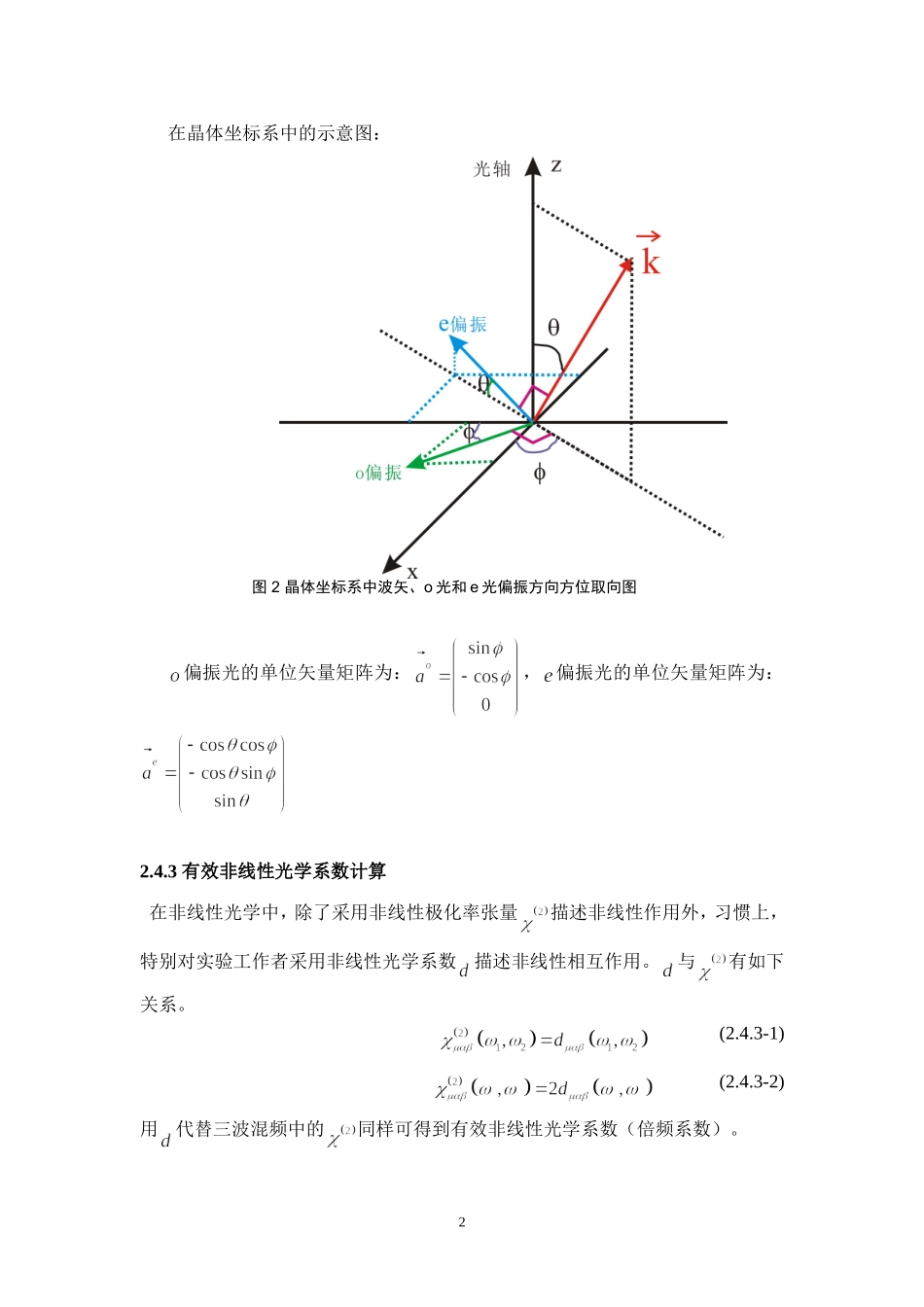
§2.4有效非线性光学系数由上节的讨论可以看到,为了高效率率地产生二次谐波,除了采用具有高非线性介质外,还应满足相位匹配条件。在实际工作中,人们引入了有效非线性系数的概念,并指出,为了有效地产生二次谐波,希望愈大愈好。2.4.1有效非线性极化率在求解三波混频的耦合波方程时,引入了有效非线性极化率。例如(2.4.1-1)有效非线性极化率除表征介质的非线性特性外,还与混频光场的偏振方向有关。有效非线性极化率实际上表示了频率为和的两个单位光电场,通过二阶极化率张量产生频率为的非线性极化强度在方向上的投影。耦合波方程的解与有效非线性极化率有关,而不与非线性极化率张量中每个元素单独发生关系。从物理上来看这是很显然的,因为所产生的非线性极化强度中只有与方向一致的分量才与偏振方向的入射光波发生耦合,而与偏振方向垂直的分量与偏振方向的入射光波不发生耦合。用耦合波方程解释:(2.4.1-2)2.4.2几种非线性匹配方式:为在晶体中达到相位匹配,参与非线性相互作用的三个光波应取特定的偏振方向。表1两类匹配四种相互作用方式I类匹配II类匹配正单轴晶体负单轴晶体图1实验室坐标系中非线性晶体中光轴、波矢及光场偏振方向示意图1在晶体坐标系中的示意图:偏振光的单位矢量矩阵为:,偏振光的单位矢量矩阵为:2.4.3有效非线性光学系数计算在非线性光学中,除了采用非线性极化率张量描述非线性作用外,习惯上,特别对实验工作者采用非线性光学系数描述非线性相互作用。与有如下关系。(2.4.3-1)(2.4.3-2)用代替三波混频中的同样可得到有效非线性光学系数(倍频系数)。图2晶体坐标系中波矢、o光和e光偏振方向方位取向图2(2.4.3-3)由本征对易对称性设定:二阶极化率张量元由三个脚标简化为两个脚标用二次谐波非线性光学系数表示,其张量形式为:(2.4.3-4)在完全克莱曼对称近似下,张量中18个元素减少到10个。等(2.4.3-5)例如类晶体KDP在空间对称作用下,独立元素会进一步减少。有效非线性系数用用矩阵运算表示:(2.4.3-6)类晶体四种相互作用方式的有效非线性光学系数计算如下:3(1)类晶体1类匹配作用方式:(2.4.3-7)(2.4.3-8)(2)类晶体II类匹配4(2.4.3-9)克莱曼对称下,,(3)类晶体I类匹配作用方式(2.4.3-10)(4)类晶体II类匹配作用方式:5(2.4.3-12)类晶体四种相互作用和有无克莱曼对称下的有效非线性光学系数表2类晶体的有效非线性系数WithKleinmansymmetryWithoutKleinmansymmetryTypeITypeIITypeITypeII可见在Kleinman对称近似下,无论正轴负轴晶体,还是I类匹配或II类匹配,有下列关系成立:(2.4.3-13)上面两式也可由Kleinman对称性和极化率张量的完全对易对称性证明。6