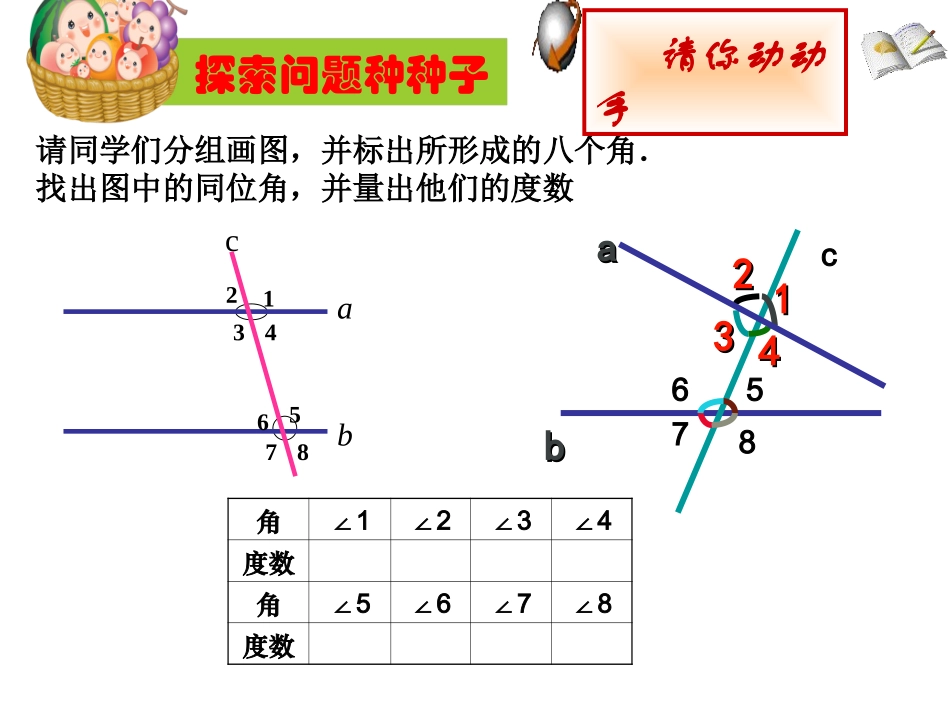
acb5.3.1平行线的性质学习目标1平行线有哪些性质?2能区分判定与性质,并能进行简单的推理和计算。重点:探索平行线的性质,并进行的推理和计算。难点:探索平行线的性质,并进行的推理和计算。角∠1∠2∠3∠4度数角∠5∠6∠7∠8度数abc13248576请同学们分组画图,并标出所形成的八个角.找出图中的同位角,并量出他们的度数请你动动手bb11223344aac5678探索问题种种子如图,直线ab∥,((11)测量)测量同位角同位角∠∠11和和∠∠55的大小,的大小,它们有什么关系?它们有什么关系?115°115°cab26134578∠∠1=5∠1=5∠ab∥请你动动手如果a与b不平行,这一规律还成立吗?角∠1∠2∠3∠4度数角∠5∠6∠7∠8度数abc13248576请同学们分组画图,并标出所形成的八个角.找出图中的同位角,并量出他们的度数请你动动手bb11223344aac5678探索问题种种子简简简简简两直线平行,同位角相等.ab32得出结论两条平行线被第三条直线所截,同位角相等.平行线性质1:几何语言表述: ab(∥已知)∴∠2=∠3(两直线平行,同位角相等)cab234猜想并讨论两直线平行,内错角、同旁内角有怎么关系呢?相互讨论一下.猜想2:两直线平行,内错角相等.心动不如行动猜想3:两直线平行,同旁内角互补.321ab(两直线平行,同位角相等)(等量代换)猜想:1=2证明: a//b(已知)∴∠2=3∠又 ∠1=3∠(对顶角相等)∴∠1=2∠性质1简两直线平行,同位角相等.如图,已知:a//b,那么1与2有什么关系?两直线平行,内错角相等.平行线的性质平行线的性质22结论结论两条平行线被第三条直线所截,内错角相等.性质发现性质发现∴∴∠∠1=2∠1=2∠((两直线平行,内错角相等 ab∥(已知)几何语言描述:简写为:b2ac11b32ac4(等量代换)猜想:2+4=180°∴2+4=180°性质1简两直线平行,同位角相等.如图,已知:a//b,那么2与4有什么关系?(两直线平行,同位角相等)证明: a//b(已知)∴∠2=3∠又 3+4=180°(邻补角定义)平行线的性质平行线的性质33结论结论两条平行线被第三条直线所截,同旁内角互补.性质发现性质发现b2ac4两直线平行,同旁内角互补.简写为:∴∴2+4=180°((两直线平行,同旁内角互补 ab∥(已知)几何语言描述:1、 AD//BC(已知)∴∴∠B=()2、 AB//CD(已知)∴∴∠D=()3、 AD//BC(已知)∴∴∠C+=180()ABCD1两直线平行,同位角相等两直线平行,内错角相等两直线平行,同旁内角互补∠D1如图,填空(6分):师生互动师生互动,,应用新知应用新知∠1∠12小青不小心把家里的梯形玻璃块打碎了,还剩下梯形上底的一部分(如图)。要订造一块新的玻璃,已经量得,你想一想,梯形另外两个角各是多少度?解: ADBC∥(梯形的定义)100,115DAADBC∴∠A+B=180°∠∠D+C=180°(∠两直线平行,同旁内角互补)∴∠B=180°-A=180°-115°=65°∠∠C=180°-D=180°-100°=80°∠又 ∠A=115°,∠D=100°(已知)师生互动师生互动,,应用新知应用新知3如图,已知直线ab∥,∠1=500,求∠2的度数(4分).abc12∴∠2=500(等量代换).解: ab∥(已知),∴∠1=2∠(两直线平行,内错角相等).又 ∠1=500(已知),变式1:已知条件不变,求∠3的度数?(4分)34反复练习反复练习,,巩固新知巩固新知变式2:已知条件不变,求∠4的度数?(5分)变式3:已知∠3=∠4,∠1=47°,求∠2的度数?(5分)解: ∠∠3=4(∠3=4(∠))∴ab∥()∴∠1=2∠(())c1234abd又 ∠1=470()∴∠2=470())当心!不要填反了!同位角相等内错角相等同旁内角互补结论条件线的关系角的关系性质角的关系线的关系判定条件结论两直线平行性质性质判定收获作业布置:•课本P22习题5.3第3题、第4题•同步练习P10第4题练习1.如图,直线ab,1=54°,2,3,4∥∠∠∠∠各是多少度?解:1234abEDCBA2.如图,D是AB上一点,E是AC上一点,∠ADE=60°∠B=60°AED=40°∠(1)DE和BC平行吗?为什么?(2)∠C是多少度,为什么?1、如图,BCD是一条直线,A=75°,1=55°∠∠,2=75°,∠求∠B的度数.E21DCBA想一想:还有其他方法吗?(三角形内角和)想一想:还有其他方法吗?(三角形内角和)课后提高:2、如图...