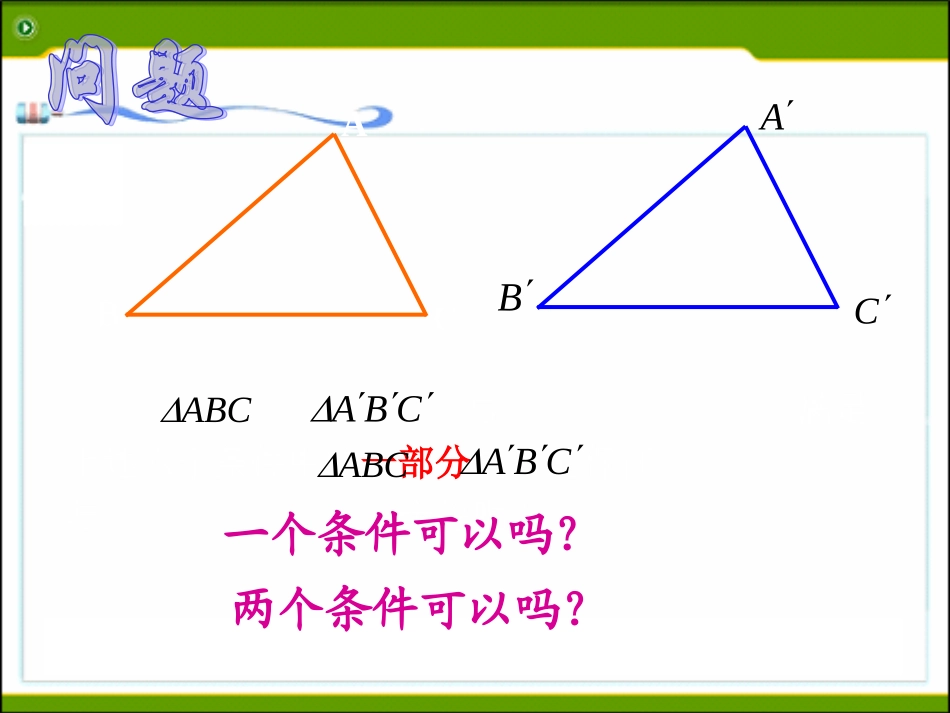
1.什么叫全等三角形?能够完全重合的两个三角形叫全等三角形.2.全等三角形有什么性质?全等三角形的对应边相等,对应角相等.3.已知,点A与A’,点B与B’,是对应顶点,试找出其中相等的边与相等的角.C'B'A'ABC≌''''''ACCA3CBBC2BAAB1=)(=)(=)('''CC6BB5AA4=)(=)(=)(,所以因为C'B'A'ABC≌ABC'A'B'C'A'B'C与满足上述六个条件中的一部分是否能保证与全等呢?CBAABCCBAABCABCABC一个条件可以吗?两个条件可以吗?三个条件呢?三个条件呢?三个条件呢?三个条件呢?探究活动探究活动1.三个角;2.三条边;3.两边一角;4.两角一边.如果给出三个条件画三角形,你能说出有哪几种可能的情况?结论:三个内角对应相等的三角形不一定全等.探究活动探究活动1.有三个角对应相等的两个三角形60o30030060o90o90o90o90o三个条件呢?三个条件呢?三个条件呢?三个条件呢?上,它们全等吗?剪下,放到把画好的=,=,=使,,再画一个先任意画出一个ABCCBA.CAACBCCBABBACBAABC''''''''''''三边相等的两个三角形会全等吗?画法:探究活动探究活动;=画线段BCCB1.'''''ΔABC.则为所求作的三角形;两弧交于点为半径画弧,、线段为圆心,、分别以'''AACABCB2..CABA3.''''、连接线段ABC三边对应相等的两个三角形全等,简写为“边边边”或“SSS”.用上面的结论可以判定两个三角形全等.用上面的结论可以判定两个三角形全等.三边对应相等的两个三角形全等.(简写成“边边边”或“SSS”)三边对应相等的两个三角形全等.(简写成“边边边”或“SSS”)结论ABCA’B’C’如何用符号语言来表达呢?,C'B'A'ABC中和在,ACCA,CBBC,BAAB''''''(SSS).C'B'A'ABC≌指指明三角形摆摆出全等的条件结论写出全等的结论例.如下图,△ABC是一个钢架,AB=AC,AD是连接A与BC中点D的支架.求证:△ABD≌△ACD.分析:要证明△ABDACD≌△,首先要看这两个三角形的三条边是否对应相等。证明:D∵是BC中点,∴BD=CD.AB=AC,BD=CD,AD=AD,∴△ABDACD≌△(SSS).在△ABD和△ACD中,∵(已知)(已证)(公共边)例题小结:一审题意标注图二缺条件要证明三指两个三角形四按序摆出三条件五得三角形全等练习:如图,C是AB的中点,AE=CF,CE=BF.求证:△ACDCBE.≌△CABEF证明:C∵是AB中点,∴AC=CB.在△ACE和△CBF中,AC=CB,(已证)AE=CF,(已知)CE=BF,(已知)∴△ACEBCF≌△(SSS).∵变式1:已知:如图,点A,D,B,C在一条直线上,且AE=CF,AC=BD,DE=BF.求证:△ADECBF.≌△证明:AC=BD,∵∴AC+CD=DB+CD,即AD=CB.在△ADE和△CBF中,∵AE=CF,(已知)AD=CB,(已证)DE=BF,(已知)∴△ADECBF(SSS).≌△ABEFDC变式2:已知:如图,点A,D,B,C在一条直线上,且AE=CF,AC=BD,DE=BF.求证:△ADE≌△CBF.ABEFDC证明:AC=BD,∵∴AC-CD=DB-CD,即AD=CB.在△ADE和△CBF中∵AE=CF,(已知)AD=CB,(已证)DE=BF,(已知)∴△ADECBF(SSS).≌△请同学们谈谈本节课的收获与体会请同学们谈谈本节课的收获与体会本节课你学到了什么?本节课你学到了什么?有什么收获?有什么收获?还存在什么没有解决的问题?还存在什么没有解决的问题?小结2.三边对应相等的两个三角形全等(简写为“边边边”或“SSS”);1.知道三角形三条边的长度怎样画三角形;3.初步学会理解证明的思路,应用“边边边”证明两个三角形全等.作业:目标检测21页基础练习;22页的6、7、10题