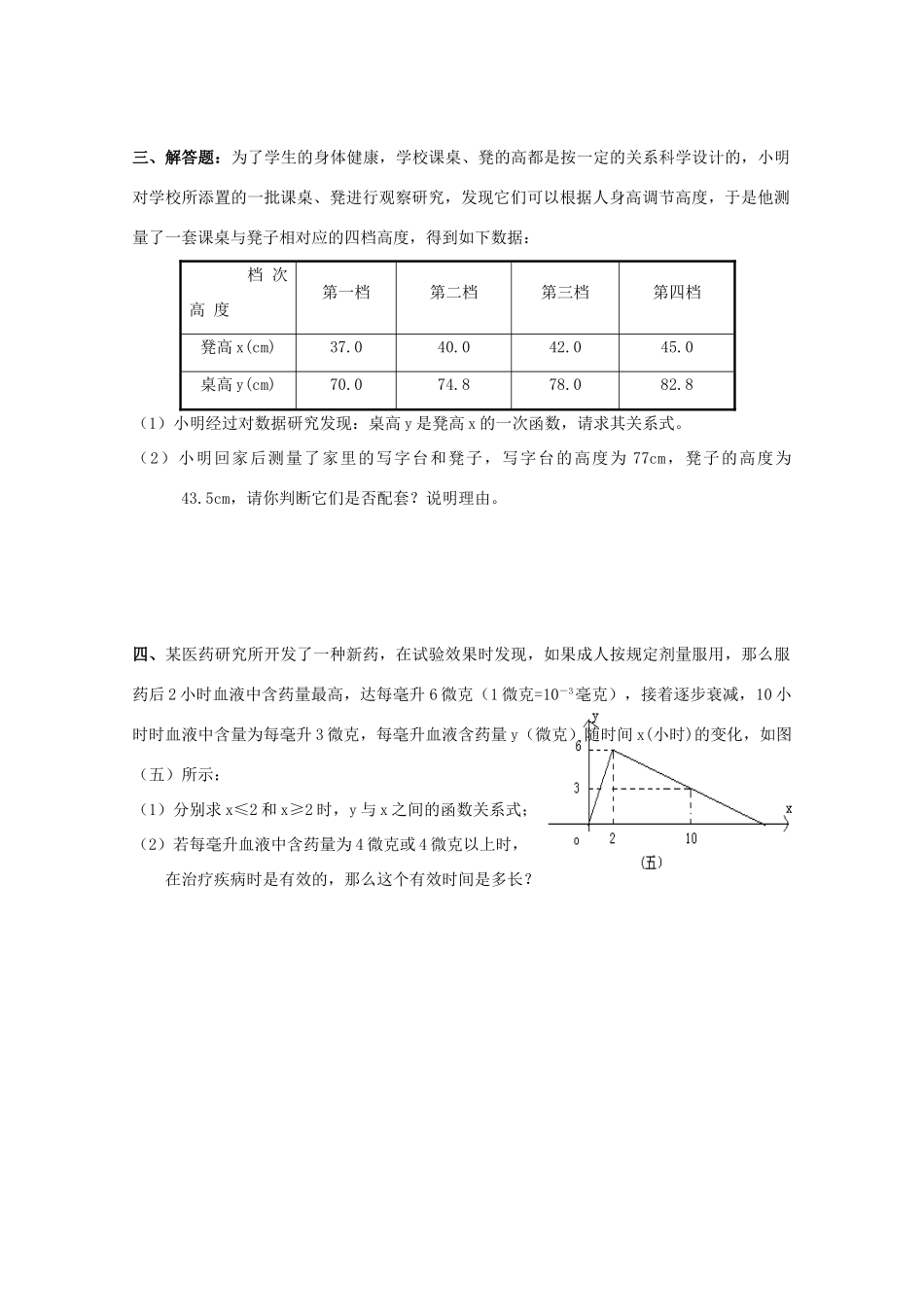
s(米)第六章一次函数一、填空题1、一次函数的图像经过点(-2,3)与(-1,1),它的解析式为。2、一次函数的图像与x轴、y轴的交点坐标分别为、。3、若函数y=(2k-4)x+3中,y随着x的增大而增大,则k.4、若直线y=ax+b经过一、二象限,那么ab0(填“>”、“<”、“=”)。5、如图,直线的解析式是。6、一次函数y=2x+b的图像与两坐标轴围成的面积为4,则b=。7、已知直线与直线y=2+1的交点的横坐标为2,与直线y=--8的交点的纵坐标为-7,则此直线的解析式是。8、abc<0,且的图像不过第四象限,则点(a+b,c)所在象限为。9、如图(二),OA、BA分别表示甲乙两名学生运动的一次函数图像,图中和分别表示运动路程和时间,根据图像判断快者的速度比慢者速度每秒快米。10、有一个水箱,它的容积为500升,水箱内原有水200升,现需将水箱注满,已知每分钟注入水10升,则水箱内水量Q(升)与时间(T)的函数关系式为。11、已知一个一次函数的图象过点(-2,3),则这个一次函数的解析式为(只需写出一个解析式即可,不必考虑所有情况)。二、选择题1、一次函数y=(2m-10)+2m-8的图像不经过第三象限,则m的取值范围是()A、m<5B、m>4C、4≤m<5D、4<m<52、点A(-5,y1)、B(-2,y2)都在直线上,则y1、y2的关系是()A、y1≤y2B、y1=y2C、y1<y2D、y1>y23、已知一次函数y=2x+a与y=-x+b的图象都经过A(-2,0),且与y轴分别交于B、C两点,则△ABC的面积为()A、4B、5C、6D、74、已知直线y=kx+b(k≠0)与x轴的交点在x轴的正半轴,下列结论(1)k>0b>0;(2)k>0b<0;(3)k<0b>0;(4)k<0b<0。其中正确的有()A、1个B、2个C、3个D、4个t(秒)5、在同一坐标系中,直线y=(k-2)x+k和直线y=kx的位置可能是()6、已知正比例函数y=(2m-1)x的图像上两点A(x1,y1)B(x2,y2),当x1<x2、y1>y2时,则m的取值范围为()A、m<2B、m>0C、m>1/2D、m<1/27、在同一直角坐标系中,对于函数(1)y=-x-1;(2)y=x+1;(3)y=-x+1;(4)y=-2(x+1)A、通过点(-1,0)的是(1)和(3)B、交点在y轴上的是(2)和(3)C、相互平行的是(1)和(2)D、关于y轴对称的是(4)和(3)8、如图(四),L甲、L乙分别是甲乙两弹簧的长y(cm)与所挂物体质量x(kg)之间的函数关系的图像,设甲弹簧每挂1kg物体伸长的长度为k甲cm,乙弹簧每挂1kg物体伸长的长度为k乙cm,则k甲、k乙的大小关系是()Ak甲>k乙Bk甲=k乙Ck甲<k乙D不能确定9、点A(x1,y1)和点B(x2,y2)在同一直线y=kx+b上,且k<0,若x1>0>x2,则y1、y2与b的关系是()Ay1>y2>bBy1<y2<bCy2>b>y1Dy1>b>y210、某市为了鼓励节约用水,按以下规定收水费:(1)每户每月用水量不超过20m3,则每立方米水费为1.2元,(2)每户用水量超过20m3,则超过的部分每立方米水费2元,设某户一个月所交水费为y(元),用水量为x(m3),则y与x的函数关系用图像表示为()三、解答题:为了学生的身体健康,学校课桌、凳的高都是按一定的关系科学设计的,小明对学校所添置的一批课桌、凳进行观察研究,发现它们可以根据人身高调节高度,于是他测量了一套课桌与凳子相对应的四档高度,得到如下数据:档次高度第一档第二档第三档第四档凳高x(cm)37.040.042.045.0桌高y(cm)70.074.878.082.8(1)小明经过对数据研究发现:桌高y是凳高x的一次函数,请求其关系式。(2)小明回家后测量了家里的写字台和凳子,写字台的高度为77cm,凳子的高度为43.5cm,请你判断它们是否配套?说明理由。四、某医药研究所开发了一种新药,在试验效果时发现,如果成人按规定剂量服用,那么服药后2小时血液中含药量最高,达每毫升6微克(1微克=10-3毫克),接着逐步衰减,10小时时血液中含量为每毫升3微克,每毫升血液含药量y(微克)随时间x(小时)的变化,如图(五)所示:(1)分别求x≤2和x≥2时,y与x之间的函数关系式;(2)若每毫升血液中含药量为4微克或4微克以上时,在治疗疾病时是有效的,那么这个有效时间是多长?