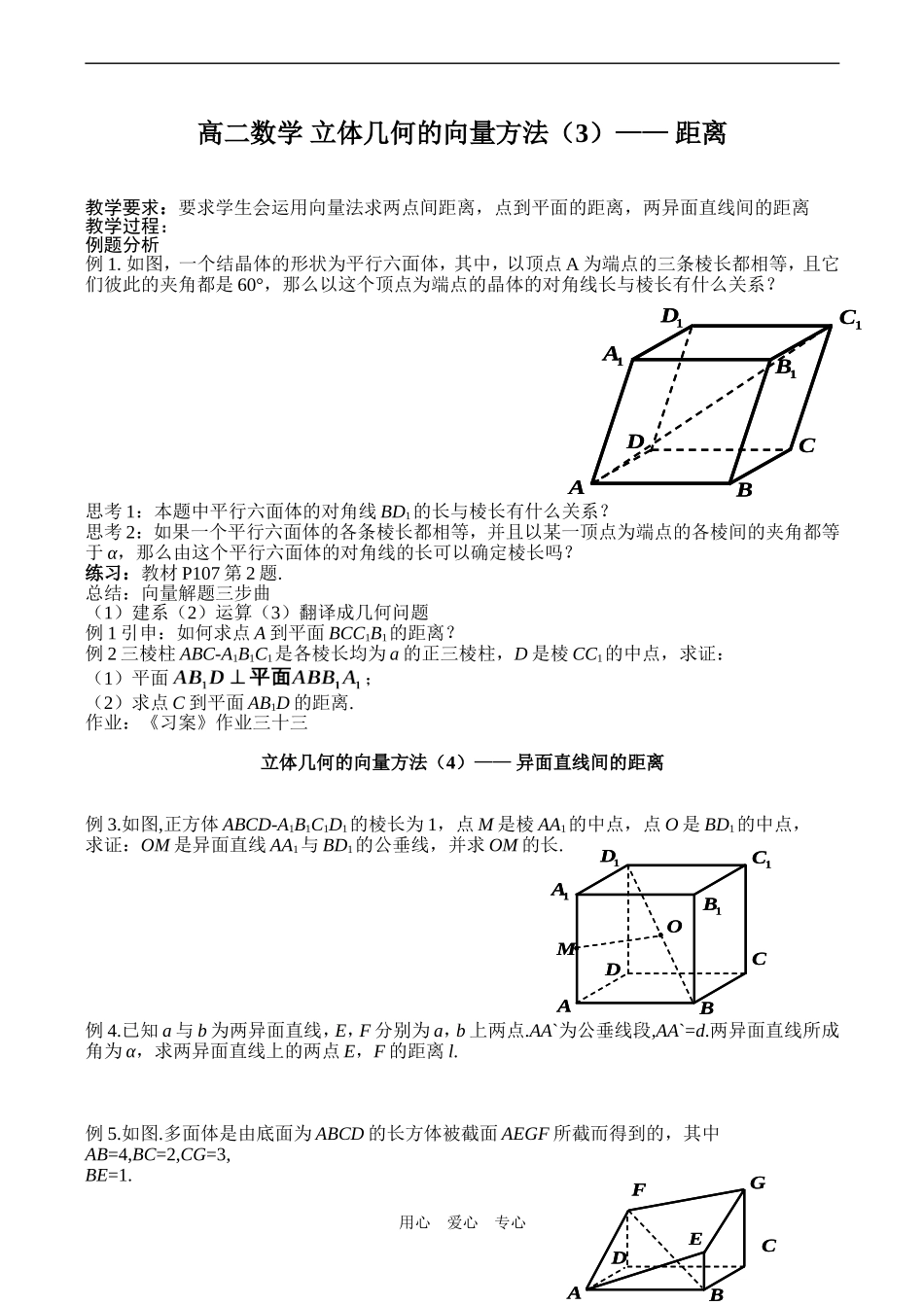
高二数学立体几何的向量方法(3)——距离教学要求:要求学生会运用向量法求两点间距离,点到平面的距离,两异面直线间的距离教学过程:例题分析例1.如图,一个结晶体的形状为平行六面体,其中,以顶点A为端点的三条棱长都相等,且它们彼此的夹角都是60°,那么以这个顶点为端点的晶体的对角线长与棱长有什么关系?思考1:本题中平行六面体的对角线BD1的长与棱长有什么关系?思考2:如果一个平行六面体的各条棱长都相等,并且以某一顶点为端点的各棱间的夹角都等于α,那么由这个平行六面体的对角线的长可以确定棱长吗?练习:教材P107第2题.总结:向量解题三步曲(1)建系(2)运算(3)翻译成几何问题例1引申:如何求点A到平面BCC1B1的距离?例2三棱柱ABC-A1B1C1是各棱长均为a的正三棱柱,D是棱CC1的中点,求证:(1)平面;(2)求点C到平面AB1D的距离.作业:《习案》作业三十三立体几何的向量方法(4)——异面直线间的距离例3.如图,正方体ABCD-A1B1C1D1的棱长为1,点M是棱AA1的中点,点O是BD1的中点,求证:OM是异面直线AA1与BD1的公垂线,并求OM的长.例4.已知a与b为两异面直线,E,F分别为a,b上两点.AA`为公垂线段,AA`=d.两异面直线所成角为α,求两异面直线上的两点E,F的距离l.例5.如图.多面体是由底面为ABCD的长方体被截面AEGF所截而得到的,其中AB=4,BC=2,CG=3,BE=1.用心爱心专心ACD1D1A1CB1BACD1D1A1CB1BACD1D1A1CB1BOMACD1D1A1CB1BOMACDBGFEACDBGFE(1)求BF的长;(2)求点C到平面AEGF的距离.例6.在长方体ABCD-A1B1C1D1中AB=4,AD=3,AA1=2,M、N分别为DC、BB1的中点,求异面直线MN与A1B的距离.作业:《学案》P89双基训练.用心爱心专心