高二数学 正切函数的性质与图象（1）精华教案VIP免费

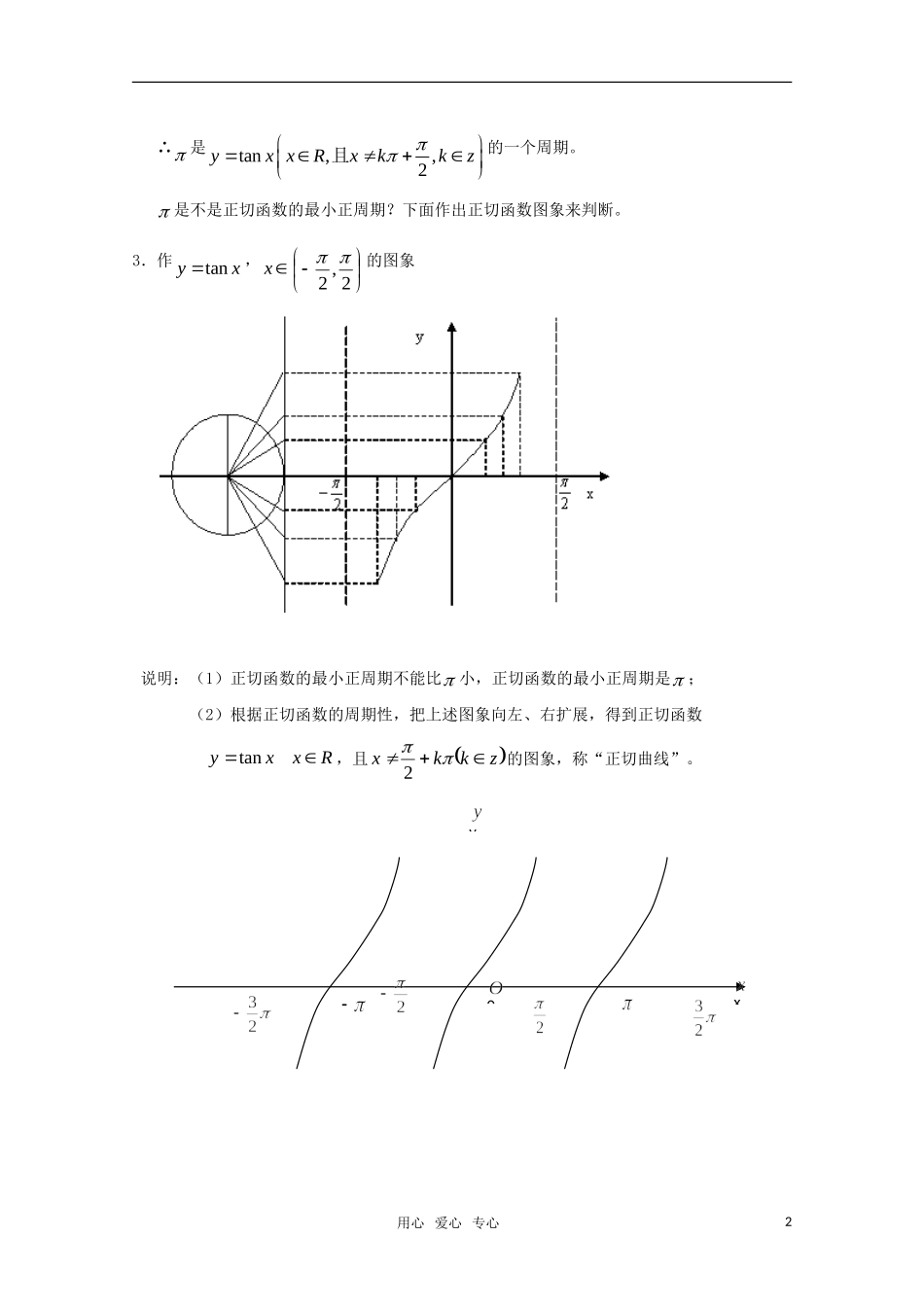
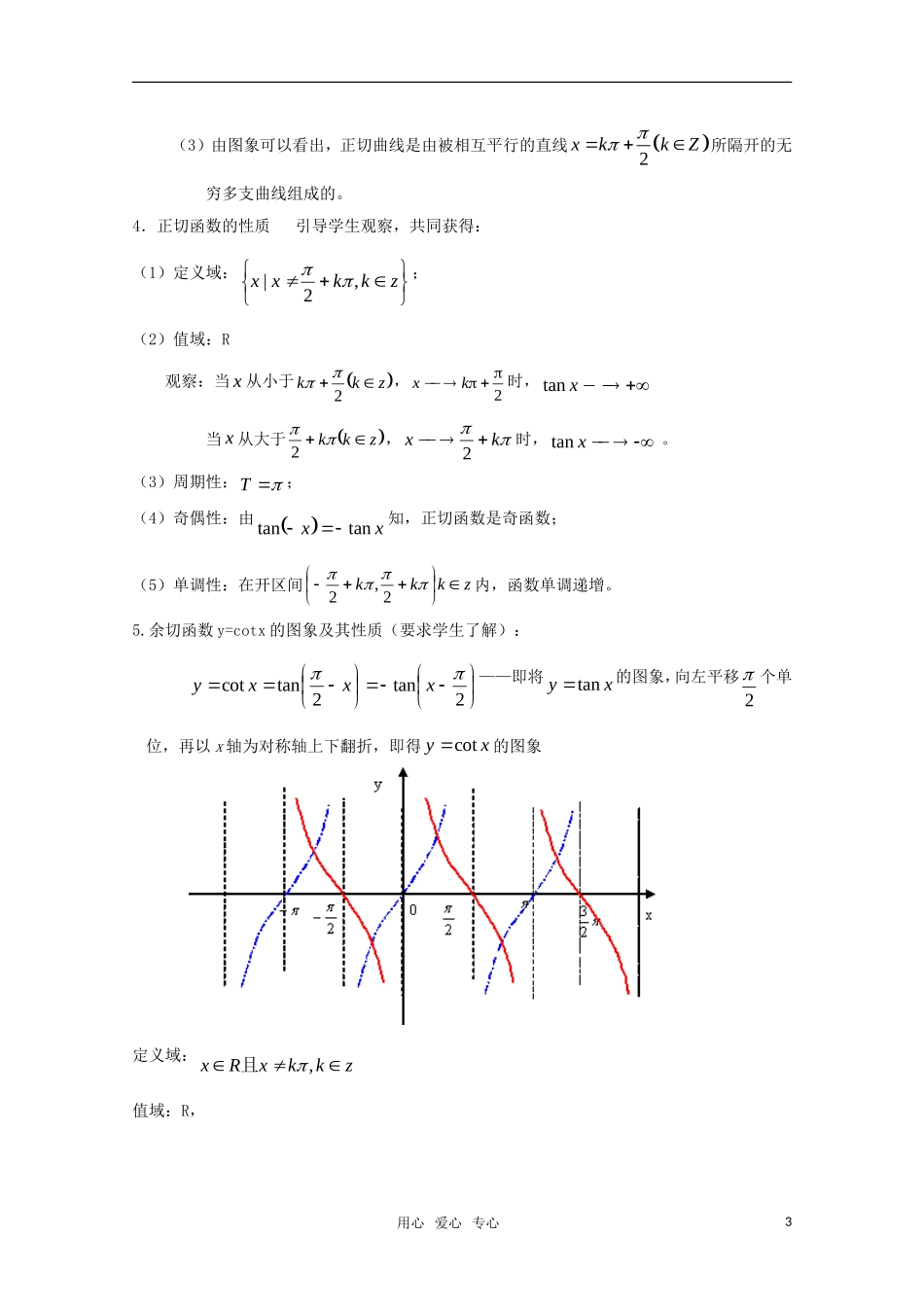
4-1.4.3正切函数的性质与图象（1）教学目的：知识目标：1.用单位圆中的正切线作正切函数的图象；2.用正切函数图象解决函数有关的性质；能力目标：1.理解并掌握作正切函数图象的方法；2.理解用函数图象解决有关性质问题的方法；德育目标：培养认真学习的精神；教学重点：用单位圆中的正切线作正切函数图象；教学难点：正切函数的性质。授课类型：新授课教学模式：启发、诱导发现教学.教具：多媒体、实物投影仪教学过程：一、复习引入：问题：正弦曲线是怎样画的？正切线?练习正切线，画出下列各角的正切线：．下面我们来作正切函数和余切函数的图象．二、讲解新课：1．正切函数tanyx的定义域是什么？zkkxx,2|2．正切函数是不是周期函数？tantan,,2xxxRxkkz且，用心爱心专心1∴是tan,,2yxxRxkkz且的一个周期。是不是正切函数的最小正周期？下面作出正切函数图象来判断。3．作tanyx，x2,2的图象说明：（1）正切函数的最小正周期不能比小，正切函数的最小正周期是；（2）根据正切函数的周期性，把上述图象向左、右扩展，得到正切函数Rxxytan，且zkkx2的图象，称“正切曲线”。用心爱心专心20yx（3）由图象可以看出，正切曲线是由被相互平行的直线2xkkZ所隔开的无穷多支曲线组成的。4．正切函数的性质引导学生观察，共同获得：（1）定义域：zkkxx,2|；（2）值域：R观察：当x从小于zkk2，2kx时，tanx当x从大于zkk2，kx2时，xtan。（3）周期性：T；（4）奇偶性：由xxtantan知，正切函数是奇函数；（5）单调性：在开区间zkkk2,2内，函数单调递增。5.余切函数y=cotx的图象及其性质（要求学生了解）：2tan2tancotxxxy——即将xytan的图象，向左平移2个单位，再以x轴为对称轴上下翻折，即得xycot的图象定义域：zkkxRx,且值域：R，用心爱心专心3当zkkkx2,时0y，当zkkkx,2时0y周期：T奇偶性：奇函数单调性：在区间1,kk上函数单调递减6.讲解范例：例1比较413tan与517tan的大小解：tan413tan4，52tan517tan，又：2,0tan,5240在xy内单调递增，517tan413tan,52tan4tan,52tan4tan即例2讨论函数4tanxy的性质略解：定义域：zkkxRxx,4|且值域：R奇偶性：非奇非偶函数单调性：在4,43kk上是增函数图象：可看作是xytan的图象向左平移4单位例3求函数y＝tan2x的定义域解：由2x≠kπ＋2，(k∈Z)得x≠2k＋4，(k∈Z)用心爱心专心4∴y＝tan2x的定义域为：｛x｜x∈R且x≠2k＋4，k∈Z｝例4观察正切曲线写出满足下列条件的x的值的范围：tanx＞0解：画出y＝tanx在(－2，2)上的图象，不难看出在此区间上满足tanx＞0的x的范围为：0＜x＜2结合周期性，可知在x∈R，且x≠kπ＋2上满足的x的取值范围为(kπ，kπ＋2)(k∈Z)例5不通过求值，比较tan135°与tan138°的大小解： 90°＜135°＜138°＜270°又 y＝tanx在x∈(90°，270°)上是增函数∴tan135°＜tan138°三、巩固与练习P．71．练习2，3，6求函数y＝tan2x的定义域、值域和周期、并作出它在区间［－π，π］内的图象解：（1）要使函数y＝tan2x有意义，必须且只须2x≠2＋ｋπ，ｋ∈Z即x≠4＋2k，ｋ∈Z∴函数y＝tan2x的定义域为｛x∈R｜，x≠24k，ｋ∈Z｝（2）设ｔ＝2x，由x≠24k，ｋ∈Z｝知ｔ≠2＋ｋπ，ｋ∈Z∴y＝tanｔ的值域为（－∞，＋∞）即y＝tan2x的值域为（－∞，＋∞）（3）由tan2（x＋2）＝tan（2x＋π）＝tan2x∴y＝tan2x的周期为2...