高一数学函数的概念 图象 表示法VIP专享VIP免费

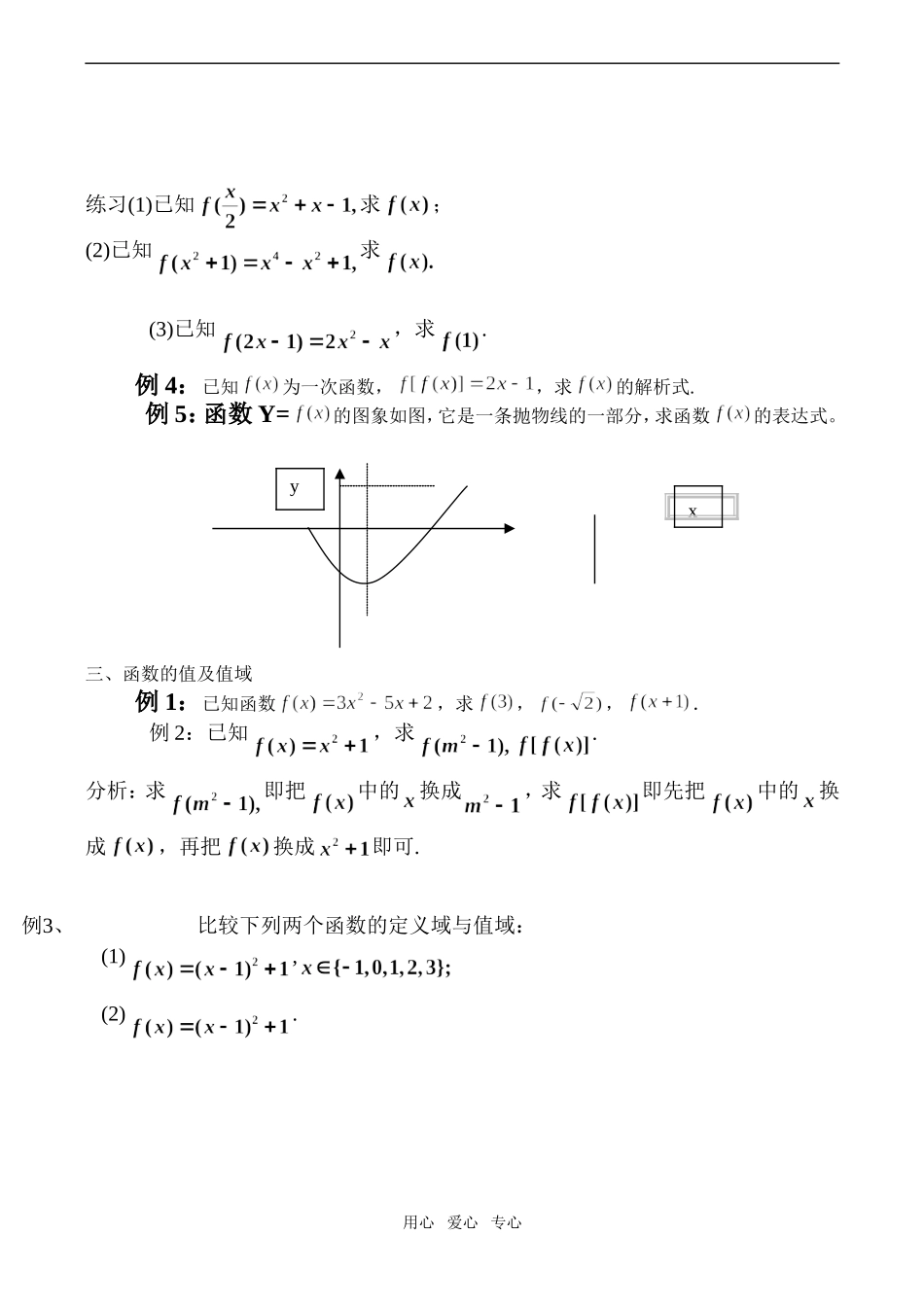
函数的概念图象表示法【教学目标】一、知识与技能1．掌握函数是特殊数集之间的对应。能熟练掌握函数的三种不同表示。2．会求一些最基本函数的定义域、值域。3.掌握函数值及解析式的求法。4.会作一些常见函数的图象，了解图象可以是散点。了解图象是数形结合的基础。5．会根据实际问题的信息特征转构建函数模型,利用该模型解决相关【教学过程】一、函数定义在初中我们学习了函数的概念，请同学们回想一下，它是怎样表述的?如何用集合语言来阐述上述问题的共同特点？函数定义：一般地，设A，B是两个非空的数集，如果按某对应法则f，对于集合A中的每一个元素x，在集合B中都有唯一的元素y和它对应，这样的对应叫做从A到B的一个函数，记为y=。例1：判断下列对应是否为函数：（1）（2）（3）解析：判断对应为函数标准是否符合函数的定义．例２：求下列函数的定义域．（１）（２）（３）解析：求函数的定义域，即求变量满足的取值范围用心爱心专心设在一个变化过程中有两个变量x与y，如果对于的每一个x值，都有唯一的y值与它对应，那么就说y是x的函数，x叫做自变量。例３：判断下列函数是否为同一函数，并说明理由．（１）（２）（３）解析：观察两函数的三要素（定义域、对应法则、值域）是否相同．思考：若两函数的定义域与值域相同时，是否为同一函数？二、函数解析式的确定例题1某市出租汽车收费标准如下:在3km以内(含3km)路程按起步价7元收费,超过3km以外的路程按2.4km收费,试写出收费额关于路程的函数解析式.例题2一家文具商店规定:凡购买铅笔51支以上(含51支)按批发价结算.而少于51支按零售价计算,批发是每购60支比零售60支少付1元.现有班长小王来购铅笔,若给全班每人买一支则必须按零售价结算,须支付m元(m为整数),但若多买10支,则可按批发价结算,恰好也是支付m元,问该班有多少学生?例3：已知函数，求的解析式．用心爱心专心练习(1)已知求；(2)已知求(3)已知，求.例4：已知为一次函数，，求的解析式.例5：函数Y=的图象如图，它是一条抛物线的一部分，求函数的表达式。三、函数的值及值域例1：已知函数，求，，．例2：已知，求.分析：求即把中的换成，求即先把中的换成，再把换成即可.例3、比较下列两个函数的定义域与值域：(1),(2).用心爱心专心xy例4、下列函数的值域：，(3)例5、求下列函数的值域：分析：该函数为分段函数，可求出各段上函数的值域，再求出它们的并集即可.例6：求函数值域．四、函数的图象例１．作出下列函数的图象：（1）f(x)=x+1,；（2）f（x）=，；（3）将下表用图象表示（4）；用心爱心专心（5）例2．设，求函数的最大值．例3．某人开车沿直线旅行，先前进了akm，到达目的地后游玩用去了一段时间，然后原路返回bkm(b