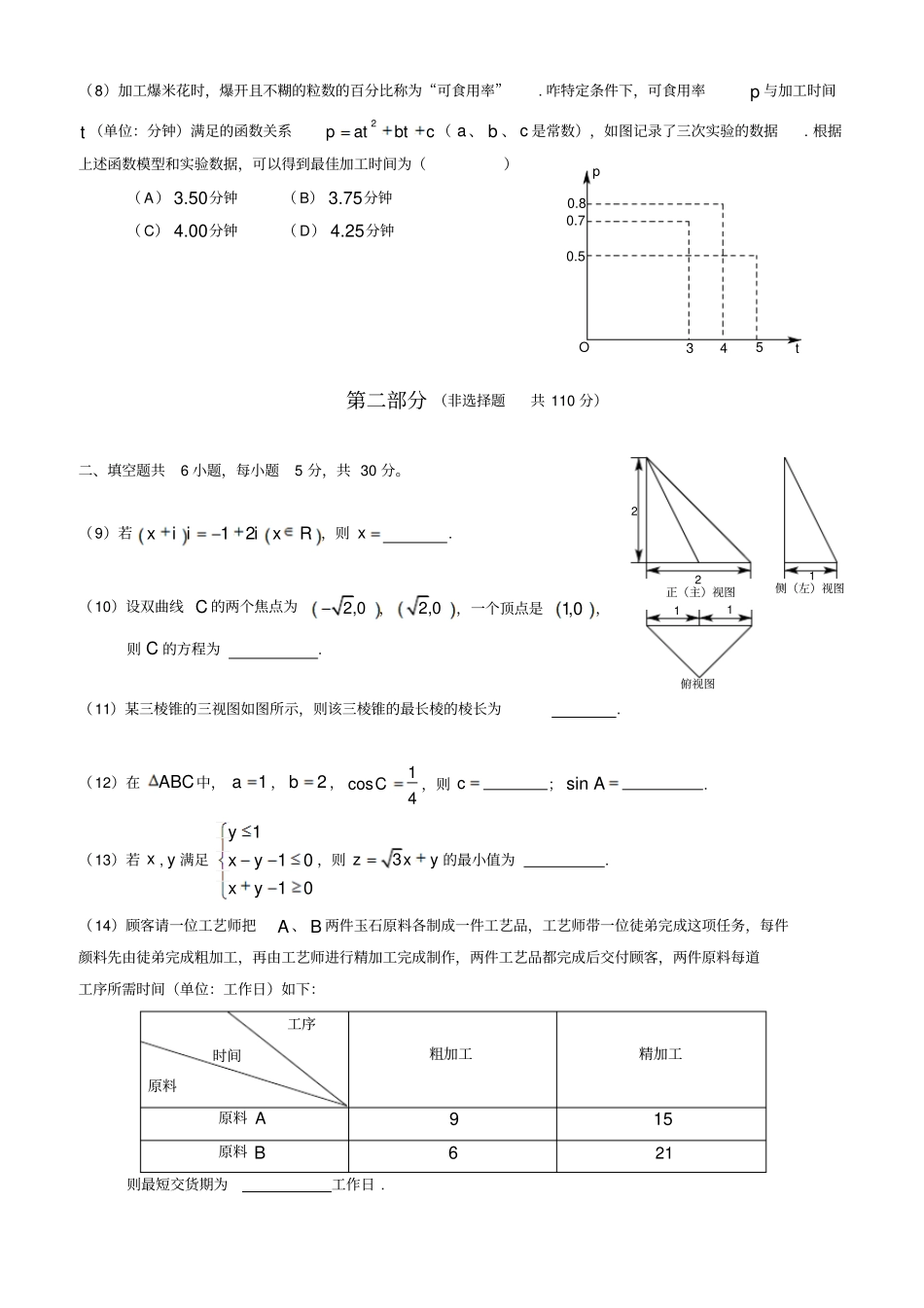
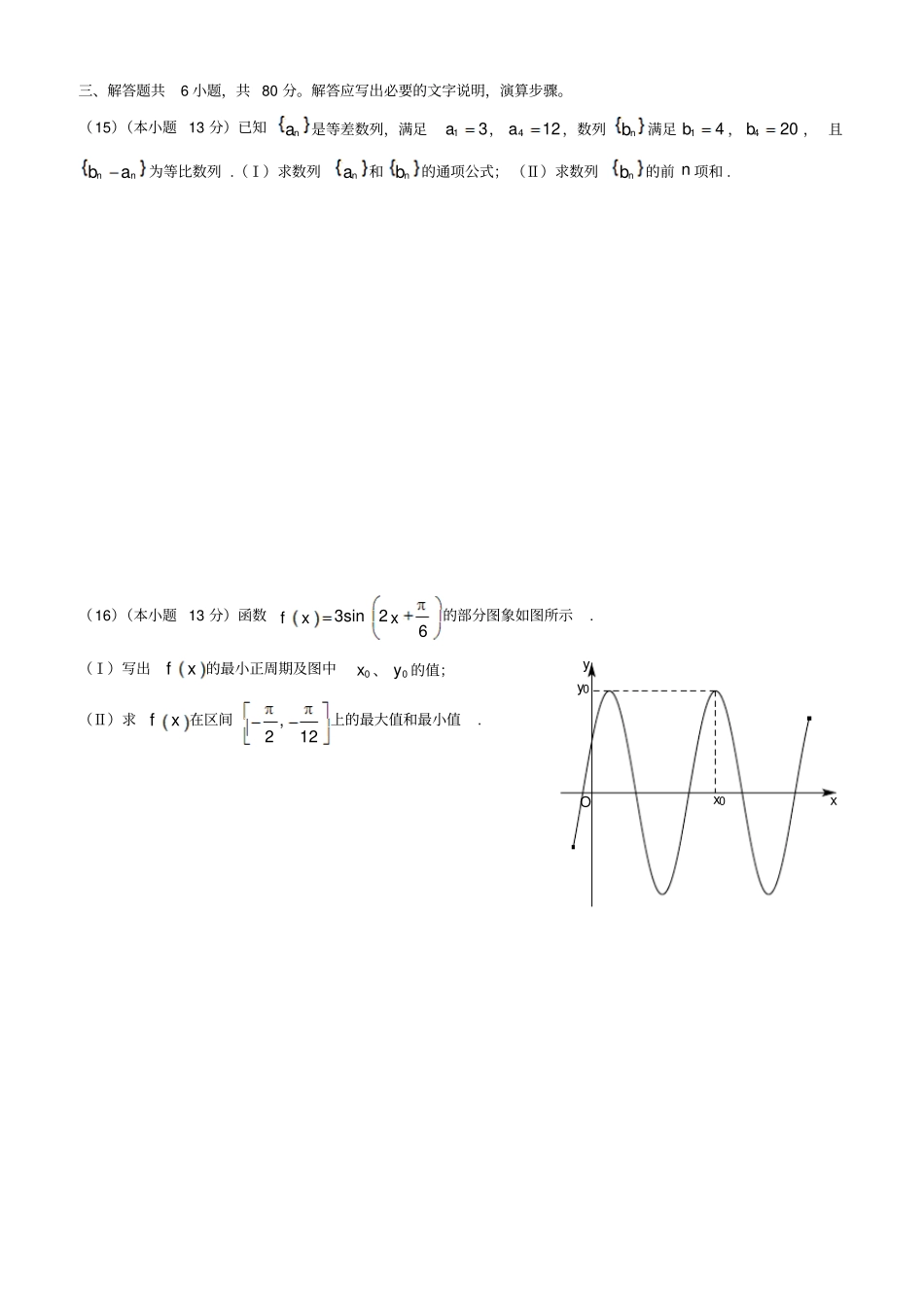
否是输出Sk=k+1S=S+2kk<3k=0,S=0结束开始绝密★启封并使用完毕前2014年普通高等学校招生全国统一考试数学(文)(北京卷)本试卷共5页,150分。考试时长120分钟,考生务必将答案答在答题卡上,在试卷上作答无效。考试结束后,将本试卷和答题卡一并收回。第一部分(选择题共40分)一、选择题共8小题,每小题5分,共40分。在每小题列出的四个选项中,选出符合题目要求的一项。(1)若集合0,1,2,4A,1,2,3B,则AB()(A)0,1,2,3,4(B)0,4(C)1,2(D)3(2)下列函数中,定义域是R且为增函数的是()(A)xye(B)yx(C)lnyx(D)yx(3)已知向量2,4a,1,1b,则2ab()(A)5,7(B)5,9(C)3,7(D)3,9(4)执行如图所示的程序框图,输出的S值为()(A)1(B)3(C)7(D)15(5)设a、b是实数,则“ab”是“22ab”的()(A)充分而不必要条件(B)必要而不必要条件(C)充分必要条件(D)既不充分不必要条件(6)已知函数26logfxxx,在下列区间中,包含fx零点的区间是()(A)0,1(B)1,2(C)2,4(D)4,(7)已知圆22:341Cxy和两点,0Am,,00Bmm,若圆C上存在点P,使得90APB,则m的最大值为()(A)7(B)6(C)5(D)4O5430.80.70.5tp(8)加工爆米花时,爆开且不糊的粒数的百分比称为“可食用率”.咋特定条件下,可食用率p与加工时间t(单位:分钟)满足的函数关系2patbtc(a、b、c是常数),如图记录了三次实验的数据.根据上述函数模型和实验数据,可以得到最佳加工时间为()(A)3.50分钟(B)3.75分钟(C)4.00分钟(D)4.25分钟第二部分(非选择题共110分)二、填空题共6小题,每小题5分,共30分。(9)若12xiiixR,则x.(10)设双曲线C的两个焦点为2,0,2,0,一个顶点是1,0,则C的方程为.(11)某三棱锥的三视图如图所示,则该三棱锥的最长棱的棱长为.(12)在ABC中,1a,2b,1cos4C,则c;sinA.(13)若x,y满足11010yxyxy,则3zxy的最小值为.(14)顾客请一位工艺师把A、B两件玉石原料各制成一件工艺品,工艺师带一位徒弟完成这项任务,每件颜料先由徒弟完成粗加工,再由工艺师进行精加工完成制作,两件工艺品都完成后交付顾客,两件原料每道工序所需时间(单位:工作日)如下:工序时间原料粗加工精加工原料A915原料B621则最短交货期为工作日.俯视图侧(左)视图正(主)视图11122三、解答题共6小题,共80分。解答应写出必要的文字说明,演算步骤。(15)(本小题13分)已知na是等差数列,满足13a,412a,数列nb满足14b,420b,且nnba为等比数列.(Ⅰ)求数列na和nb的通项公式;(Ⅱ)求数列nb的前n项和.(16)(本小题13分)函数3sin26fxx的部分图象如图所示.(Ⅰ)写出fx的最小正周期及图中0x、0y的值;(Ⅱ)求fx在区间,212上的最大值和最小值.Oyxy0x0(17)(本小题14分)如图,在三棱柱111ABCABC中,侧棱垂直于底面,ABBC,12AAAC,E、F分别为11AC、BC的中点.(Ⅰ)求证:平面ABE平面11BBCC;(Ⅱ)求证:1//CF平面ABE;(Ⅲ)求三棱锥EABC的体积.(18)(本小题14分)从某校随机抽取100名学生,获得了他们一周课外阅读时间(单位:小时)的数据,整理得到数据分组及频数分布表和频率分布直方图:(Ⅰ)从该校随机选取一名学生,试估计这名学生该周课外阅读时间少于12小时的概率;(Ⅱ)求频率分布直方图中的a,b的值;(Ⅲ)假设同一组中的每个数据可用该组区间的中点值代替,试估计样本中的100名学生该周课外阅读时间的平均数在第几组(只需写出结论)组号分组频数102,6224,8346,17468,225810,2561012,1271214,681416,291618,2合计100C1B1A1FECBA阅读时间ba频数组距18161412108642O(19)(本小题14分)已知椭圆C:2224xy.(Ⅰ)求椭圆C的离心率;(Ⅱ)设O为原点,若点A在直线2y,点B在椭圆C上,且OAOB,求线段AB长度的最小值.(20)(本小题13分)已知函数3()23fxxx.(Ⅰ)求()fx在区间[2,1]上的最大值;(Ⅱ)若过点(1,)Pt存在3条直线与曲线()yfx相切,求t的取值范围;(Ⅲ)问过点(1,2),(2,10),(0,2)ABC分别存在几条直线与曲线()yfx相切?(只需写出结论)绝密★考试结束前2014年普通高等学校招生全国统一考试数学(文)(北京卷)参考答案一、选择题(共8小...