§231成比例线段(2)VIP免费

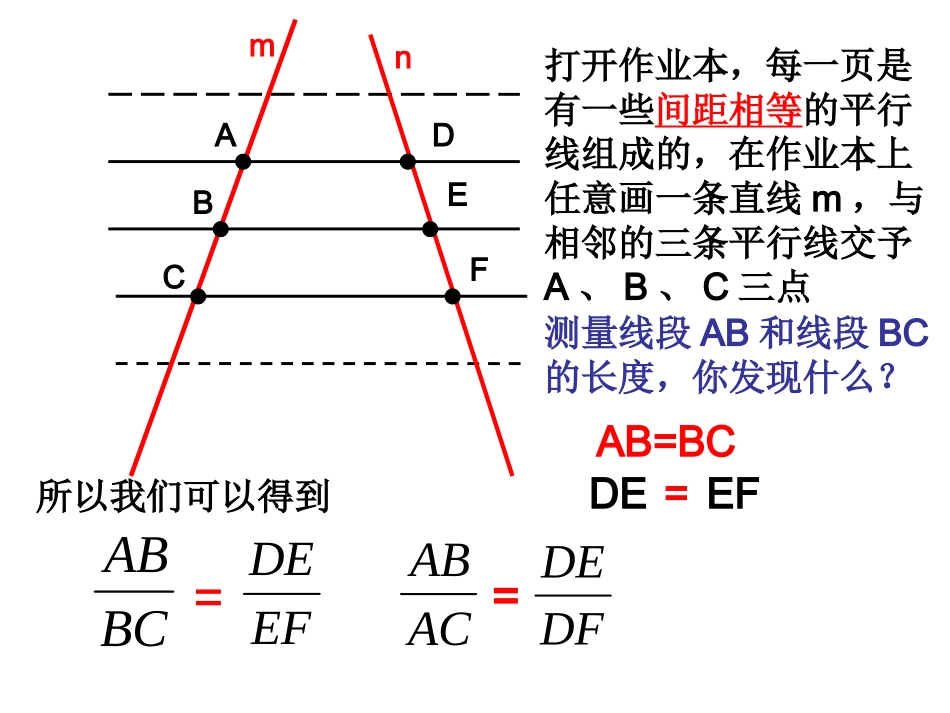
学习目标：•1、理解并掌握平行线分线段成比例这一基本事实及其推论。•2、能运用平行线分线段成比例这一基本事实及推论解决问题。ABC测量线段AB和线段BC的长度，你发现什么？打开作业本，每一页是有一些间距相等的平行线组成的，在作业本上任意画一条直线m，与相邻的三条平行线交予A、B、C三点mAB=BCnDEFDEEF=所以我们可以得到BCABEFDE=ACABDFDE=做一做:选择作业本上不相邻的三条平行线ACBFEDmn指出AC、CB、FE、ED这四条线段的长度有什么关系?EDFECBAC我们发现：CBACEDFE3131思考：我们还可以发现哪些线段成比例？41FDFEABAC43FDEDABCB两条直线被一组平行线所截,所得的对应线段成比例（简称平行线分线段成比例）FECADB几何语言：1l2l3lmnECFEDBADlll321////推论：想一想，从图中你还能得出哪些线段为成比例线段？FCFEABADFCECABDB)(下上下上)(全上全上)(全下全下当A点与F点重合时，就成了一个三角形的特殊情形，此时AD、DB、AE、EC这四条线段之间会有怎样的关系呢？ADBFECADB(F)ECECAEDBAD结论：)(下上下上AFAEABAD)(全上全上ACECABDB)(全下全下ABCDEECAEDBADBC//DEACAEABADACECABDB几何语言：L1DABECL2L3思考：如图当直线m、n相交于第二条平行线上某点时，是否也有类似的成比例线段呢？我们发现结论：ACEAABDAECEADBDAECACDBABmnDABCE延长线上的点、是分别、中，如图：在CABAEDABCBCDE//ACEAABDAECEADBDAECACDBAB几何语言:推论：推论：平行于三角形一边的直线截其他两边(或两边的延长线），所得的对应线段成比例。推论的几何语言：∵DEBC∥ADAEABAC∴————＝（推论）ABCDEDABCE做一做教材p53FDABCE找出图中成比列的线段已知：BCAF////DE...,,EFFCADACEFFCAEABADACAEABABCDE————练习一:1、判断题:如图:DEBC,∥下列各式是否正确D:————＝ADAEABAC()C:————＝ADACAEAB()B:————＝ADBDAECE()A:ADAB＝AEAC()2、填空题:如图:DEBC,∥已知:2＝——AEAC—5＝——ADAB求:——ABCED的长。求如图例BC.6,3,4////3,321EFDEABlllBOEOFOBOFADO,ACBE,CDE4。求证：于点交于点交连结延长线上的一点，为平行四边形的边如图点例练习：P55----1、2练习二:ABDCEECBCDC————＝ABCDE1、如图:已知DEBC,∥AB=14,AC=18，AE=10，求：AD的长。2、如图:已知ABBD⊥，EDBD⊥，垂足分别为B、D。求证：ACCB=4，BEAB=AABCDEC达标检测题:1、如图:已知DEBC,∥AB=5,AC=7，AD=2，求：AE的长。BDE2、已知∠A=E=60°∠求：BD的长。———23小结•一、基本事实：两条直线被一组平行线所截,所得的对应线段成比例（简称平行线分线段成比例）•二、推论：推论：平行于三角形一边的直线截其他两边(或两边的延长线），所得的对应线段成比例。课后作业：•课本p55练习