平面向量二级结论集合 (1)VIP免费

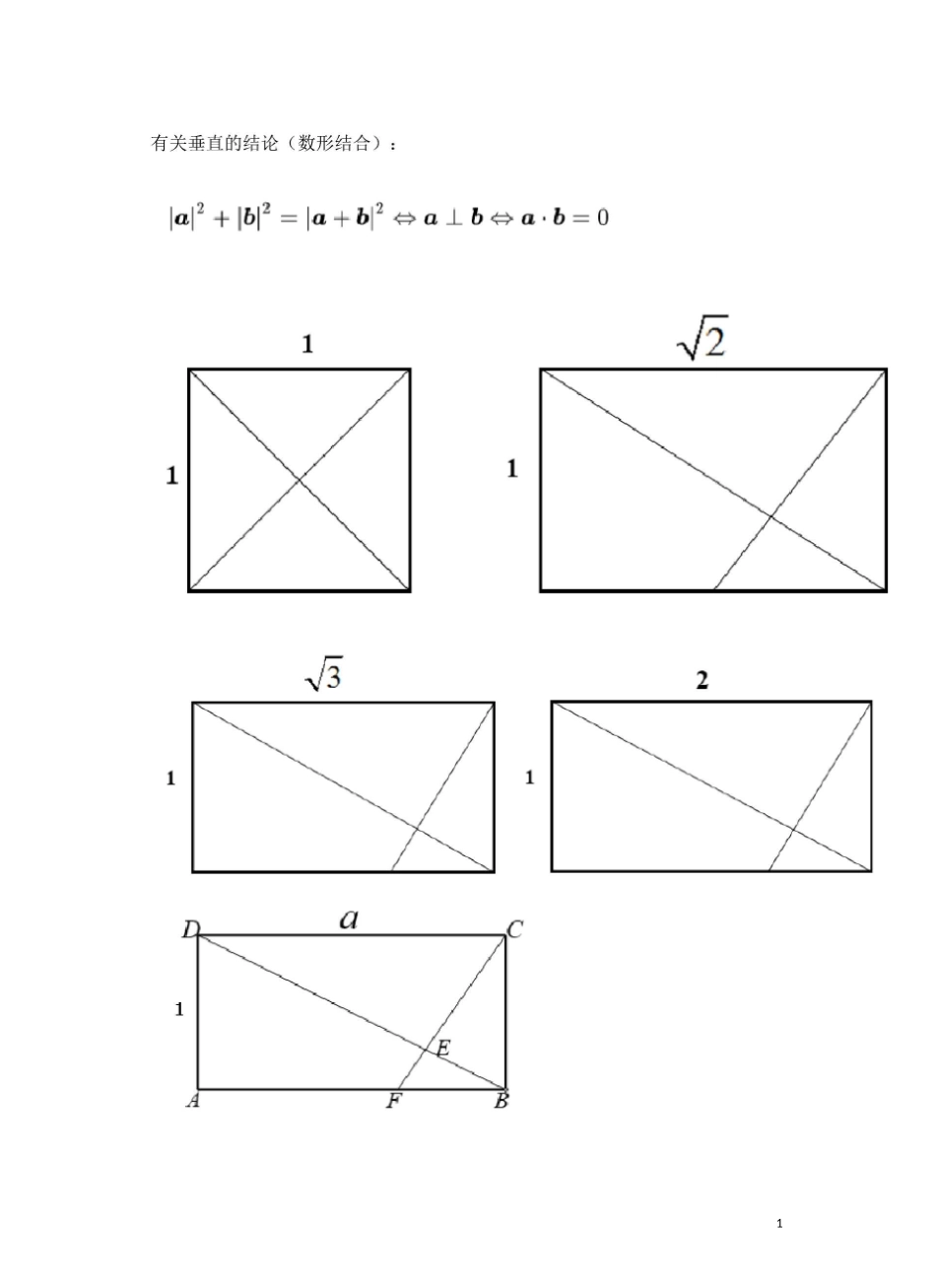
12满足BD和CF垂直的时候，有下列的数量关系:AB=c?FBDB=+1)弱AF=-1)FBDE=A2EB向量绝对值不等式：―J―t—#|5|-|&|<|2+6|<|2|+|&|求数量积的两个重要模型:后续再利用条件进行化简。3极化恒等式三角形模型：极化恒等式的作用主要在于:它可以将两个向量的数量积转化为这两个向量的"和向量〃与〃差向量”,因此，当两个向量的“和向量”或“差向量”为定向量时，常常可以考虑利用极化恒等式进行转化求解.极化恒等式平行边形模型:42■&=[(S+&)2_(a—b)2向量的数量积可以表示为以这组向量为邻边的平行四边形的“和对角线”与“差对角线”平方差的平行四边形两条对角线的平分和等于两条邻边平分和的两倍.以此类推至L三角形，若AM是AABC的中线「AB2+AC2=2(AM-+BM2)举个栗子：在△ABC中「设点幷是AB边上一走点满足P^B=^AB，且对于AB边上点P恒有PB^PC^P^B”P^C「则A+LABC=90°B+ABAC=90°AB=ACAC=BC公式变形:举个栗子：-、-¥在平面上』ABi丄AB2,OBI~'*1—OP\<-.则OA的取值范围是"-、OB=It-、-'-、AP=ABr+AB2若D5矩形的两个小性质：(1)已知距形ABCD’O是平面任意—点,则OA.QC^OB.OD(2)已知矩形ABCD,O是平面任意一点」则+|0C|2=\OBf+|OD|26需要说明的是，对角线向量定理①和后文所出现的式子②③既适用于平面向量也适用于空间向量。当用于空间向量的适合大家把这个图形想象成为三棱锥D-ABC即可，AC和BD成为三棱锥的一组对棱，如下图所示。7这就是对角线向量定理尼表明四边形的两条对角线对应向量的数量积可用四条边的长度表示。推论1:式子②表明，当对角线相互垂直时，四边形两组对边的平方和相等。推论2:向量中三点共线的结论:K艮G三点共住＜^0D=mOA十nOC.OB=0D（同时除以m+rt）m+n若匕A、B三点共纸.则存在实数入■使QP=XOA+jiOB仇卄匸"•特别地苣P为纸®AB的中点时，OP=|o4+jofe8910定比分点公式的向量表示与坐标表示:若点P分向量XB所成的比为入「则庆=。丛+入0B1+A设尸仙V）f4佃〕,的）,3（旳］劭），点卩分可星AB所成的比为人则》_/—眄_y_甘\翊一兀y'2-y向量与三角形四心:AB!AC\|AB|sinB|ic|sin(7AB\或柞出高AD后知两分式的分母相尊sinC［百线AO过△乂阁重心.也+胧+m3三角形的重心坐标公式；设X(3C1^1),j?(a；2.y2)1C(X3^3)则△虫EG的重心坐标九/却十1；2+叼三角形的重心分中线两段线段长度比为2:1,且分的三个三角形面积相使OA+ofe3+OC取最小值时的O鼠为^ABC的重心•三角形三条中线交点。OA+OB+OC=0^0是ME。的尋心(1)重心在△ABC中，角A}B.C所对的边分别是a7b.c若AO-XsinBCDA3等1112垂直平分线的交点，到三个顶点的距离相等。13AO^AB=^\AB^AO^AC=BO^BC=^\BC^£(b)组応金=^\AB\2十^-|Jc,|2,44BO^BE=^\AB^十扌歲巴co^cb=^-|BC|2+^-\AC\44(c)袒AO-DC=^\ACf-^\^3\\BO■AC=-^\BA\\忌爲=*|品血OS\BOC:S^AOC:14(5)外心和垂心结合0为其外心,H为其垂」则OH=OA+OB+0C奔驰定理:-、-+―>rS^BOC*OA+S^AOC-OB+SMOJ?•OC=0推论:若x\y\z=S^mG:S^AQC:S^AQB^则濒+yOB+zOC=6⑴O是^ABC的重心=1'.1'A^OA+OB^OC=G(2〕O是MBC的内心台S^XBQC:SAAOC:=a:b■.aOA+bOB十cOC=0⑶Q是^ABC的外心令S'EUC:S^AOG:5X+OE=sin2A::sin2COsin2A0A+"口2B0B+sin2C0C=015⑷O是△百的垂心今SABOC；S[\AOC:S^AQB=tanS;tanB；tanC-¥->―¥_).OtanAOA+tanBOB+tanCOC=0证明：如图0为三角形的垂心「心=箸3=需二tanA:tanB—DB:ADS也BGC；SMOG=DB:ADSgg:=taml:tan5同理得S^AOG:S^4OS=tanB:tanCSABQC:=tanA:tan(7-■.S'Bg:S^A0C:S^A0S=tan.4:tanB:tanC梅涅劳斯(Menelaus)定理简介(作为平面几何内容对向量很有贡献):如果一直线顺次与三角形ABC的三边AB、BC、CA或其延长线交于M、N、K三点，则:FMB7K证明：过顶点B作AC的平行线与截线交于E,则有:NC故BNCKAKBECK=-^―-三角形面积公式的向量表a=0B=b=（Z2,lta）>则=-Mil平面上二蛊不共线「设龟(%473=\^la|2|^|2-(a*^)2AMAKBN_BEMMB16