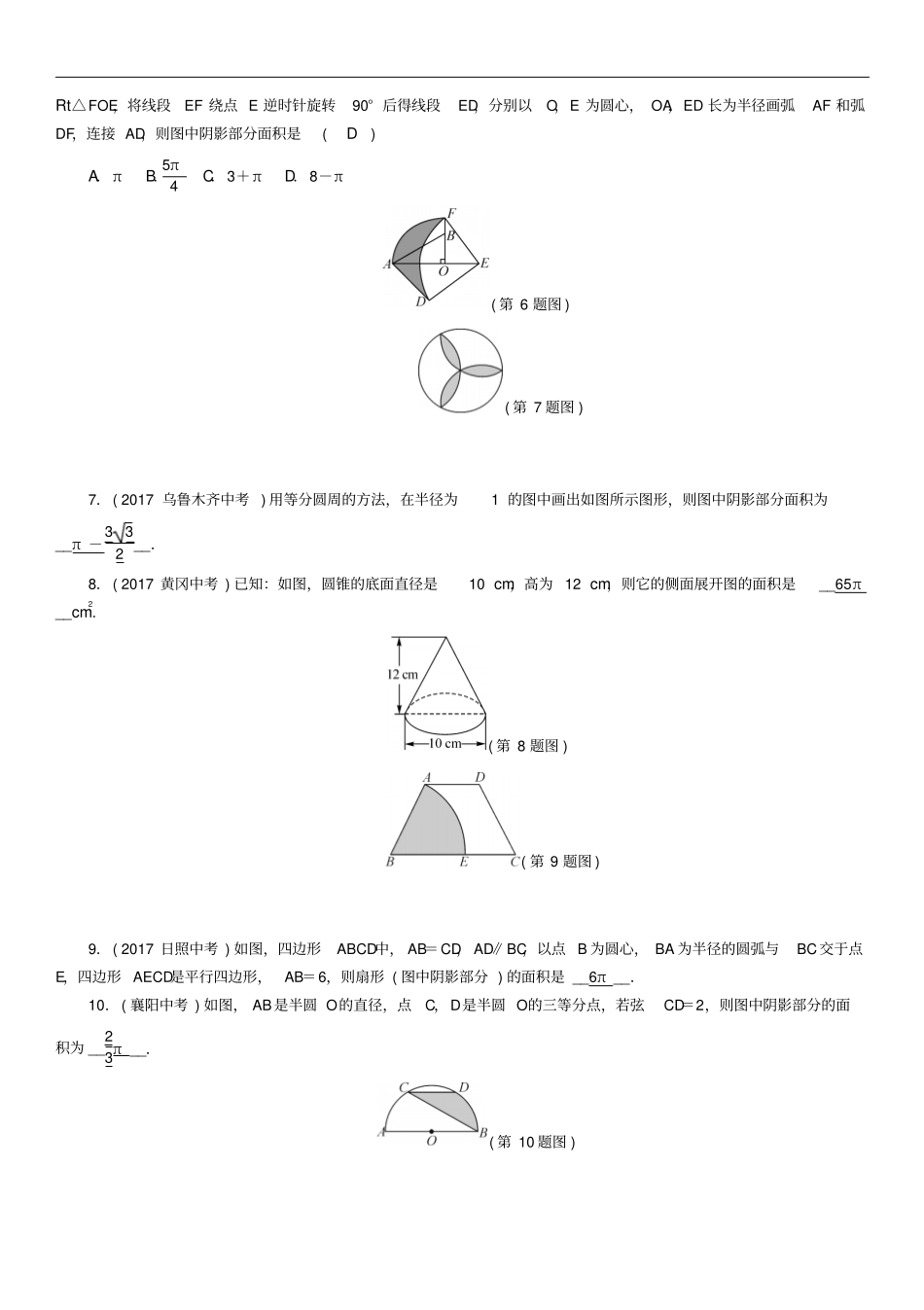
第三节与圆有关的计算1.(2017宿迁中考)若将半径为12cm的半圆形纸片围成一个圆锥的侧面,则这个圆锥的底面圆半径是(D)A.2cmB.3cmC.4cmD.6cm2.(2017临沂中考)如图,AB是⊙O的直径,BT是⊙O的切线,若∠ATB=45°,AB=2,则阴影部分的面积是(C)A.2B.32-14πC.1D.12+14π3.(2017达州中考)以半径为2的圆的内接正三角形、正方形、正六边形的边心距为三边作三角形,则该三角形的面积是(A)A.22B.32C.2D.34.(2017莱芜中考)将半径为3cm的圆形纸片沿AB折叠后,圆弧恰好能经过圆心O,用图中阴影部分的扇形围成一个圆锥的侧面,则这个圆锥的高为(A)A.22cmB.2cmC.10cmD.32cm(第4题图)(第5题图)5.(2017深圳中考)如图,在扇形AOB中,∠AOB=90°,正方形CDEF的顶点C是AB︵的中点,点D在OB上,点E在OB的延长线上,当正方形CDEF的边长为22时,阴影部分的面积为(A)A.2π-4B.4π-8C.2π-8D.4π-46.(桂林中考)如图,在Rt△AOB中,∠AOB=90°,OA=3,OB=2,将Rt△AOB绕点O顺时针旋转90°后得Rt△FOE,将线段EF绕点E逆时针旋转90°后得线段ED,分别以O,E为圆心,OA,ED长为半径画弧AF和弧DF,连接AD,则图中阴影部分面积是(D)A.πB.5π4C.3+πD.8-π(第6题图)(第7题图)7.(2017乌鲁木齐中考)用等分圆周的方法,在半径为1的图中画出如图所示图形,则图中阴影部分面积为__π-332__.8.(2017黄冈中考)已知:如图,圆锥的底面直径是10cm,高为12cm,则它的侧面展开图的面积是__65π__cm2.(第8题图)(第9题图)9.(2017日照中考)如图,四边形ABCD中,AB=CD,AD∥BC,以点B为圆心,BA为半径的圆弧与BC交于点E,四边形AECD是平行四边形,AB=6,则扇形(图中阴影部分)的面积是__6π__.10.(襄阳中考)如图,AB是半圆O的直径,点C,D是半圆O的三等分点,若弦CD=2,则图中阴影部分的面积为__23π__.(第10题图)(第11题图)11.(2017河南中考)如图,在扇形AOB中,∠AOB=90°,以点A为圆心,OA的长为半径作OC︵交AB︵于点C,若OA=2,则阴影部分的面积为__3-13π__.12.(2017济宁中考)如图,正六边形A1B1C1D1E1F1的边长为1,它的六条对角线又围成一个正六边形A2B2C2D2E2F2,如此继续下去,则正六边形A4B4C4D4E4F4的面积是__318__.13.(2017广州中考)如图,圆锥的侧面展开图是一个圆心角为120°的扇形,若圆锥的底面圆半径是5,则圆锥的母线l=__35__.(第13题图)(第14题图)14.(2017达州中考)如图,矩形ABCD中,E是BC上一点,连接AE,将矩形沿AE翻折,使点B落在CD边F处,连接AF,在AF上取点O,以O为圆心,OF长为半径作⊙O与AD相切于点P.若AB=6,BC=33,则下列结论:①F是CD的中点;②⊙O的半径是2;③AE=92CE;④S阴影=32.其中正确结论的序号是__①②④__.15.(2017永州中考)如图,在平面直角坐标系中,点A的坐标(-2,0),△ABO是直角三角形,∠AOB=60°.现将Rt△ABO绕原点O按顺时针方向旋转到Rt△A′B′O的位置,则此时边OB扫过的面积为__14π__.(第15题图)(第16题图)16.(2017遵义红花岗一模)如图,将含60°角的直角三角板ABC绕顶点A顺时针旋转45°后得到△AB′C′,点B经过的路径为BB′︵.若∠BAC=60°,AC=1,则图中阴影部分的面积是__π2__.17.(2017玉林中考)如图,在⊙O中,AB是直径,点D是⊙O上一点,且∠BOD=60°,过点D作⊙O的切线CD交AB的延长线于点C,E为AD︵的中点,连接DE,EB,交于点F.(1)求证:四边形BCDE是平行四边形;(2)已知图中阴影部分面积为6π,求⊙O的半径r.解:(1)连接EO. ∠BOD=60°,∴∠AOD=120°,∴BD︵=12AD︵. E为AD︵的中点,∴AE︵=DE︵=BD︵,∴∠EOD=60°.又OE=OD,∴∠EDO=60°,∴DE∥AB,即DE∥BC. CD是⊙O的切线,∴OD⊥CD.由垂径定理得OD⊥EB,∴BE∥CD,∴四边形BCDE是平行四边形;(2) S△DEF=S△BOF,∴S阴影=S扇形OBD,即60°×π×r2360°=6π,∴r=6.18.(昆明中考)如图,AB是⊙O的直径,∠BAC=90°,四边形EBOC是平行四边形,EB交⊙O于点D,连接CD并延长交AB的延长线于点F.(1)求证:CF是⊙O的切线;(2)若∠F=30°,EB=4,求图中阴影部分的面积.(结果保留根号和π)解:(1)连接OD. 四边形OBEC是...