电磁学第8章习题VIP免费

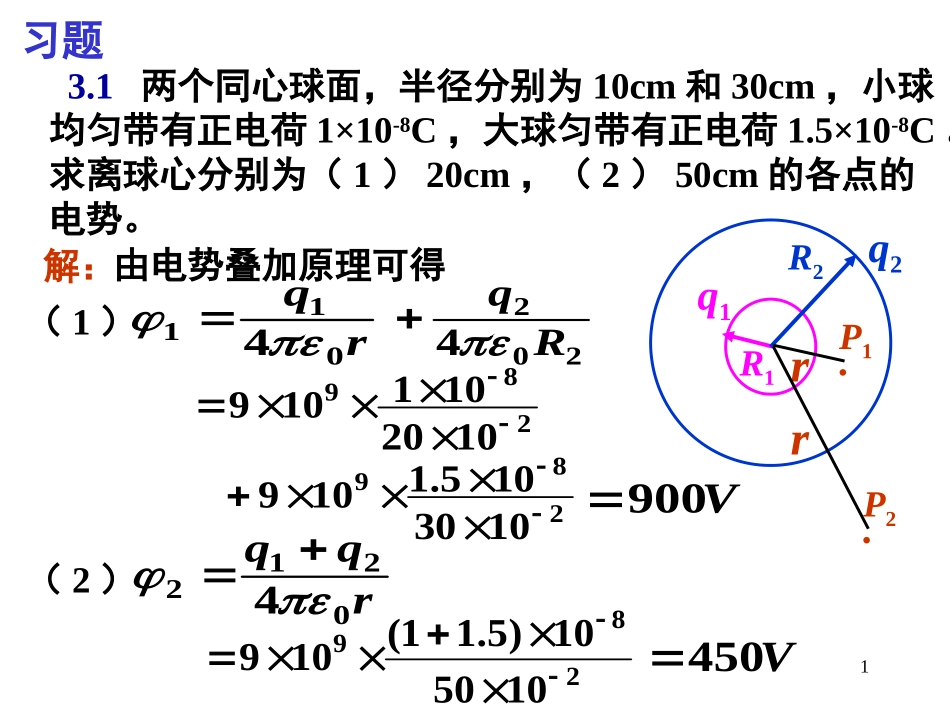
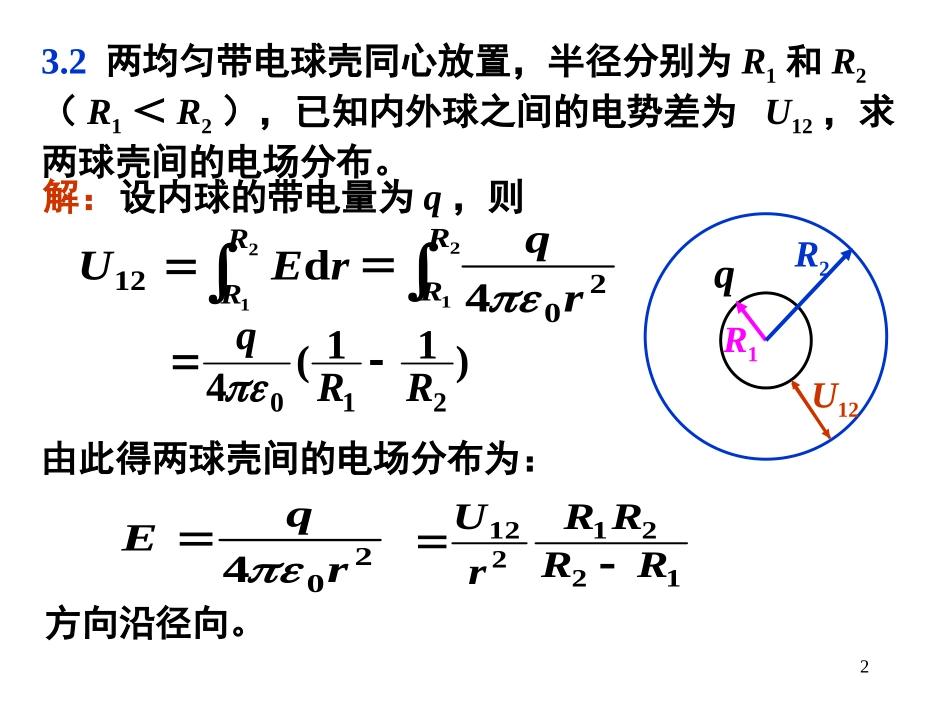
1R1q1R2q23.1两个同心球面，半径分别为10cm和30cm，小球均匀带有正电荷1×10-8C，大球匀带有正电荷1.5×10-8C。求离球心分别为（1）20cm，（2）50cm的各点的电势。解：由电势叠加原理可得（1）P1●rrq01142024Rq28910201011092891030105.1109V900（2）P2●rrqq02124289105010)5.11(109V450习题23.2两均匀带电球壳同心放置，半径分别为R1和R2（R1＜R2），已知内外球之间的电势差为U12，求两球壳间的电场分布。R1R2U12解：设内球的带电量为q，则q21d12RRrEU21204RRrq)11(4210RRq由此得两球壳间的电场分布为：204rqE1221212RRRRrU方向沿径向。33.3一均匀带电细杆，长为l＝15cm，线电荷密度λ＝2.0×10-7C/m。求：解：（1）细杆延长线上与杆的一端相距a=5.0cm处电势；（2）细杆中垂线上与细杆相距b=5.0cm处电势。lxalx001)(4d（1）沿杆取x轴，杆的x轴反向端点取作原点，由电势叠加原理，可得所给点的电势为（2）利用3.5题的结果，可得alaln400.50.150.5ln100.210979)V(105.232/4/2/4/ln4222202llbllb2/154/1552/154/155ln100.2109222279)V(103.4343.4半径为R的圆盘均匀带电，面电荷密度为σ。求此圆盘轴线上的电势分布（1）利用原书例3.4的结果用电势叠加法；（2）利用原书第1章例1.6的结果用场强积分法。解：由电势叠加原理，整个电圆在x处的电势（1）半径为r，宽度为dr的带电圆环在圆盘轴线上离盘心x处的电势为2204d2dxrrr（2）整个带电圆盘在x轴上的电场分布式为Rxrrr02204d2d])(1[22/1220xRxE)(2220xRx5由场强积分可求出x处的电势为xxEd)(2220xxRxxxRxd))(1(22/122063.5用电势梯度法求上面题中x＞0各点的电场强度。解：已知沿x轴有aaxaax22220ln4在x轴上,0dyEy0zEz2202axxaxEEx73.6一边长为工的正三角形，其三个顶点上各放置q，－q和－2q的点电荷，求此三角形重心上的电势。将一电量为＋Q的点电荷由无限远处移到重心上，外力要做多少功？解：重心上的电势为rqrqrq00004244AAaqaq0023)211(343所求外力做的功为)(0QaqQQ002383.7地球表面上空晴天时的电场强度约为100V/m。（1）此电场的能量密度多大？（2）假设地球表面以上10km范围内的电场强度都是这一数值，那么在此范围内所储存的电场能共是多少kW·h？解：220EeeEhwRW24（1）（2）68326106.3104.41010)104.6(4h)(kW103.64)J/m(104.4382)100(1085.82129习题集一、选择题：3.8一“无限大”带负电荷的平面，若设平面所在处为电势零点，取x轴垂直带电平面，原点在带电平面处，画出其周围空间各点电势U随距离平面的位置坐标x变化的关系曲线为：xo-σ分析：“无限大”均匀带负电荷平面的电场分布，如右图：场强大小为：02E电势分布：xoUExxdEUx0x<0处，E>0，U>0;x>0处，E<0，U>0.电势分布图线应是103.9在点电荷＋q的电场中，若取图中P点处为电势零点，则M点的电势为[]分析：由电势定义PMMrEUd因此，正确答案是D项。D.80aq（D）;80aq（B）;40aq（A）;40aq（C）a++qM●P●arrqaad4220aarq20)1(4rq08113.10电荷面密度为+σ和-σ的两块“无限大”均匀带电的平行平板，放在与平面相垂直的x轴上的+a和-a位置上，设坐标原点o处电势为零，则在-a＜x＜+a区域的电势分布曲线为[]x-a-σo+a●σ+分析：两“无限大”均匀带电平面之间的电场分布，如右图：E其大小表示为：0E电势分布（原点o处电势为零）：ExxEUx0dx<0处，E<0，U<0;x>0处，E<0，U>0.电势分布图线应是C项。x0Ux-ao+a●C123.11一带电可作为点电荷处理的条件是[]分析：是C项。（A）...