电磁学第一章习题答案VIP免费

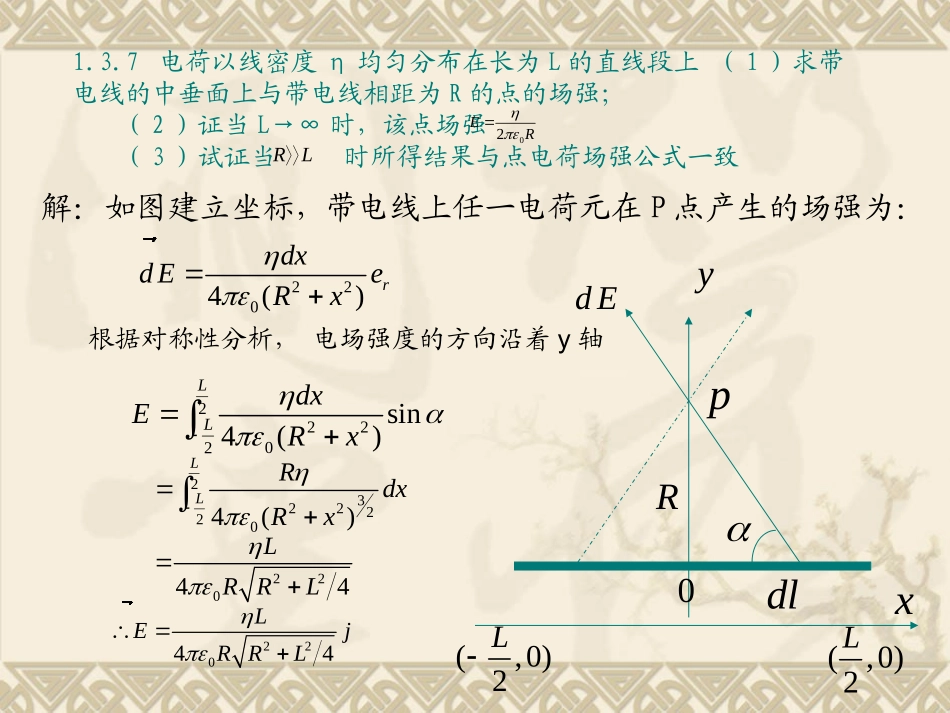
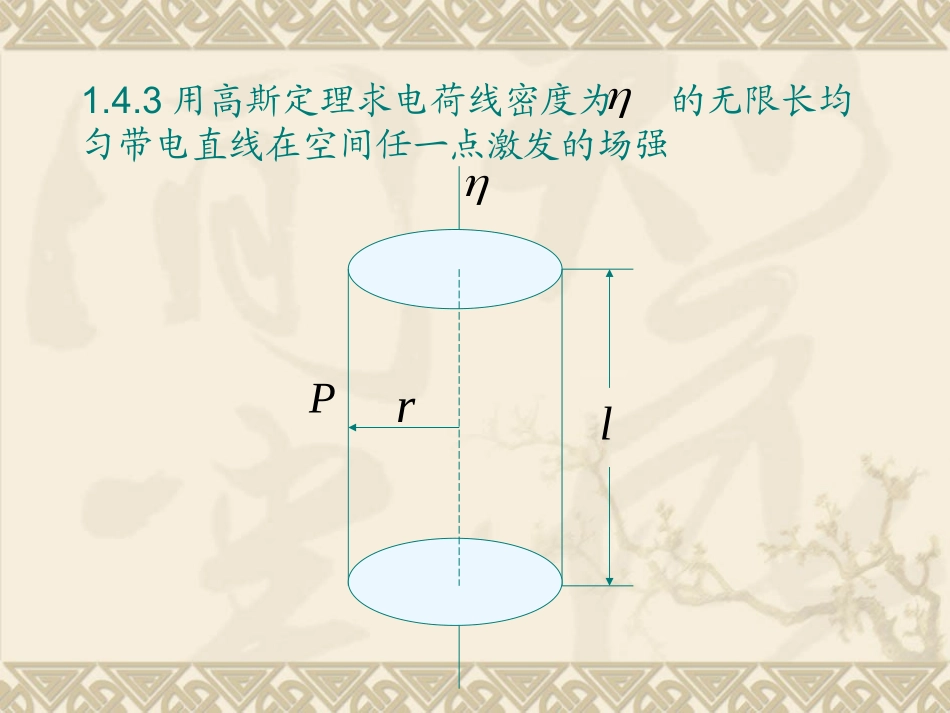
1.3.7电荷以线密度η均匀分布在长为L的直线段上（1）求带电线的中垂面上与带电线相距为R的点的场强；（2）证当L→∞时，该点场强（3）试证当时所得结果与点电荷场强公式一致02ER解：如图建立坐标，带电线上任一电荷元在P点产生的场强为：2204()rdxdEeRx�(,0)2LydE�pR0dl(,0)2LxLR根据对称性分析，电场强度的方向沿着y轴22202sin4()LLdxERx23222204()LLRdxRx22044LRRL22044LEjRRL�（2）当L→∞时22220044414LERRLRRL当L→∞时220RL00242ERR（3）当RL时220044LqERR其中Lq与点电荷公式一致2224RLRR1.4.3用高斯定理求电荷线密度为的无限长均匀带电直线在空间任一点激发的场强Plr解：根据对称性分析，无限长均匀带电直线在空间任一点产生的场强与棒垂直，呈辐射状。如图所示以带电直线为轴线过P点作一封闭的圆柱面。长度L是任意的。由高斯定理：coscoscosEdSEdSEdSEdS�侧面上底下底0L上下底面上2cos0侧面上场强夹角0cos10cos2LEdSEdSErL�侧面02Er1.4.6电荷以体密度分布在半径为R的球内，其中为常量，r为球内某点与球心的距离0(1)rR0（1）求球内外的场强（以r代表从球心到场点的矢量）（2）r为多大时场强最大？该点场强max?EP0POR解（1）与r是线性关系。在球内过点做一个半径为r的与带电球同心的球面为高斯面如图，根据对称性分析，此球面上的场强大小相等，方向与的一致。0(1)rR0r由高斯定理：0qEdS�24EdSrE�内320044()3rrErR内00(134)3rErR内304()3rrR200(1)4rrqrdrR当r＞R时，即在球外过任一点p仍做球形高斯面。由高斯定理得24EdSrE�外外3200134RrE外302012REr外23000(1)413RqrRrdrR（2）03(1)032dErdrR内23rR0max09REr越大，单调减小，因而球外场强无极值E�外1.6.3附图中A与O、O与B、B与D的距离皆为L，A点有正电荷q，B点有负电荷-q（1）把单位正电荷从O点沿半圆OCD移到D点，电场力做了多少功？（2）把单位负电荷从D点沿AD的延长线移到无穷远，电场力做了多少功？CqAO2LDBLq根据电位叠加原理：001()04qqULL（1）电场力把单位正电荷（即）从O点沿OCD移到D点所做的功：01q001()436DqqqULLL00000()(0)66OCDDqqAqUUqLL场力把单位负电荷（即）从D点移到无穷远所作的功：01q000()()66DDqqAqUUqLL