平行线的判定与性质课件VIP免费

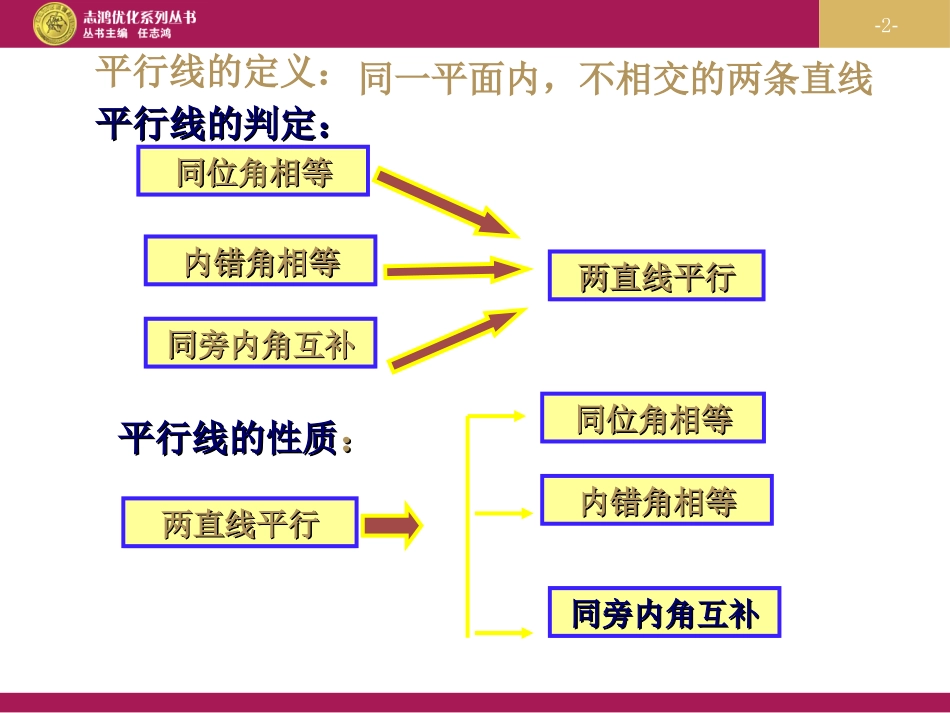
平行线的判定与性质习题课-2-平行线的性质平行线的性质：：两直线平行两直线平行同位角相等同位角相等内错角相等内错角相等同旁内角互补同旁内角互补平行线的判定：平行线的判定：两直线平行两直线平行同位角相等同位角相等内错角相等内错角相等同旁内角互补同旁内角互补平行线的定义：同一平面内，不相交的两条直线-3-复习复习图形图形条件条件结论结论理由理由同位角同位角内错角内错角同旁内角同旁内角2123)42(18042互补与a//ba//ba//b同位角相等两直线平行内错角相等两直线平行同旁内角互补两直线平行122324））））））abababccc平行线的判定平行线的判定-4-图形图形条件条件结论结论理由理由同位角同位角内错角内错角同旁内角同旁内角23)42(18042互补与a//ba//b内错角相等两直线平行同旁内角互补两直线平行122324））））））abababccc平行线的性质平行线的性质21a//b同位角相等两直线平行21a//b同位角相等两直线平行21a//b同位角相等两直线平行21a//b同位角相等两直线平行a//b21两直线平行同位角相等a//b23两直线平行内错角相等同旁内角互补a//b)42(18042互补与两直线平行-5-复习引入ABCDEFHGABCDEFHGABCDEFHGF形模式Z形模式C形模式-6-感悟模式ABCDE∵DEBC∥∴∠B＝∠ADE∴∠C＝∠AED∴∠B＋∠BDE＝180°∴∠C＋∠CED＝180°∴DEBC∥∵∠B＝∠ADE∵∠C＝∠AED∵∠B＋∠BDE＝180°∵∠C＋∠CED＝180°名称:塔形模式-7-探索模式ABCDE名称:塔形模式∵∠B＝∠ADE∴DEBC∥∴∠C＝∠AED∠B＋∠BDE＝180°∠C＋∠CED＝180°角的关系直线平行判定确定其它角的关系性质结论-8-感悟模式∵ABCD∥∴∠B＝∠D∴∠C＝∠A∵∠B＝∠D∵∠C＝∠A∴DEBC∥名称:蝶形模式ABCDO-9-探索模式ABCDO名称:蝶形模式∵∠B＝∠D∴ABCD∥∴∠C＝∠A角的关系直线平行判定确定其它角的关系性质结论-10-应用模式ABCDEF1231ABCDEABCDF3CDEF2塔形模式Z形模式塔形模式-11-应用模式如图,若AB∥DF,∠2＝∠A,试确定DE与AC的位置关系,并说明理由.ABCDEF2ABCDFACDEF2-12-应用模式如图,图中包含哪些基本模式?ABCDEFOBCDFOABDEOBDEFOABCD-13-应用模式已知,如图AB∥EF∥CD,AC∥BD,BC平分∠ABC,则图中与∠EOD相等的角有()个.A.2B.3C.4D.5ABCDEFOD-14-应用模式①下图中包含哪些基本模式?②已知:1∠＝∠2,C∠＝∠D,求证:DFAC∥③已知:A∠＝∠F,C∠＝∠D,求证:DBEC∥ABCDEF12-15-辨一辨1.两直线平行，同旁内角相等2.两条直线被第三条直线所截，同位角相等3.内错角的对顶角相等（）（）（）×××-16-填空：(1)∵2=(已知),(）.(2)∵ABDF(已知),2+=180(）.(3)∵ACDE(已知),C=().（4）∵=DFC(∠已知),∴∥（）∴∠2=BED∠（）(5)(∵已知),ABFD(∥）.ACBDEF123内错角相等，两直线平行两直线平行，同旁内角互补两直线平行，同位角相等DFCDEACAED1ABFD同位角相等，两直线平行两直线平行，内错角相等∠A-17-2.如图：已知：ab∥，∠12=45﹕∠﹕，则∠1=度。12abc3.如图：已知：∠1=2∠，则∠C+∠____=____度21DCBA4.已知ABEFCD∥∥，∠B=400，∠C=1500，则∠BEC=度ABEFCD8018010D-18-1.已知：如图：∠1=∠2,∠C=70，∠ADE=70°问BD平分∠ABC吗？21AEDCB∵∠C=70，解：∴∠ADE=C∠∴DEBC∥又∵∠1=2∠∴∠1=DBC∠∴BD平分∠ABC∠ADE=70（已知）∴∠2=DBC∠(两直线平行，内错角相等）（等量代换）（同位角相等，两直线平行）（已知）(等量代换）（角平分线的意义）-19-2.如图：在△ABC中,点E,Ｇ分别是AB,AC上的点，AD⊥BC,EF⊥BC,点F,D是垂足，且∠1=∠2，试说明:AB∥DG.┏┏21GCDFBEA-20-小结反馈我们在本节课的学习中发现了哪些新方法?弄懂了哪些新知识?-21-巩固作业课本第24页,第13,14,15题。-22-再见