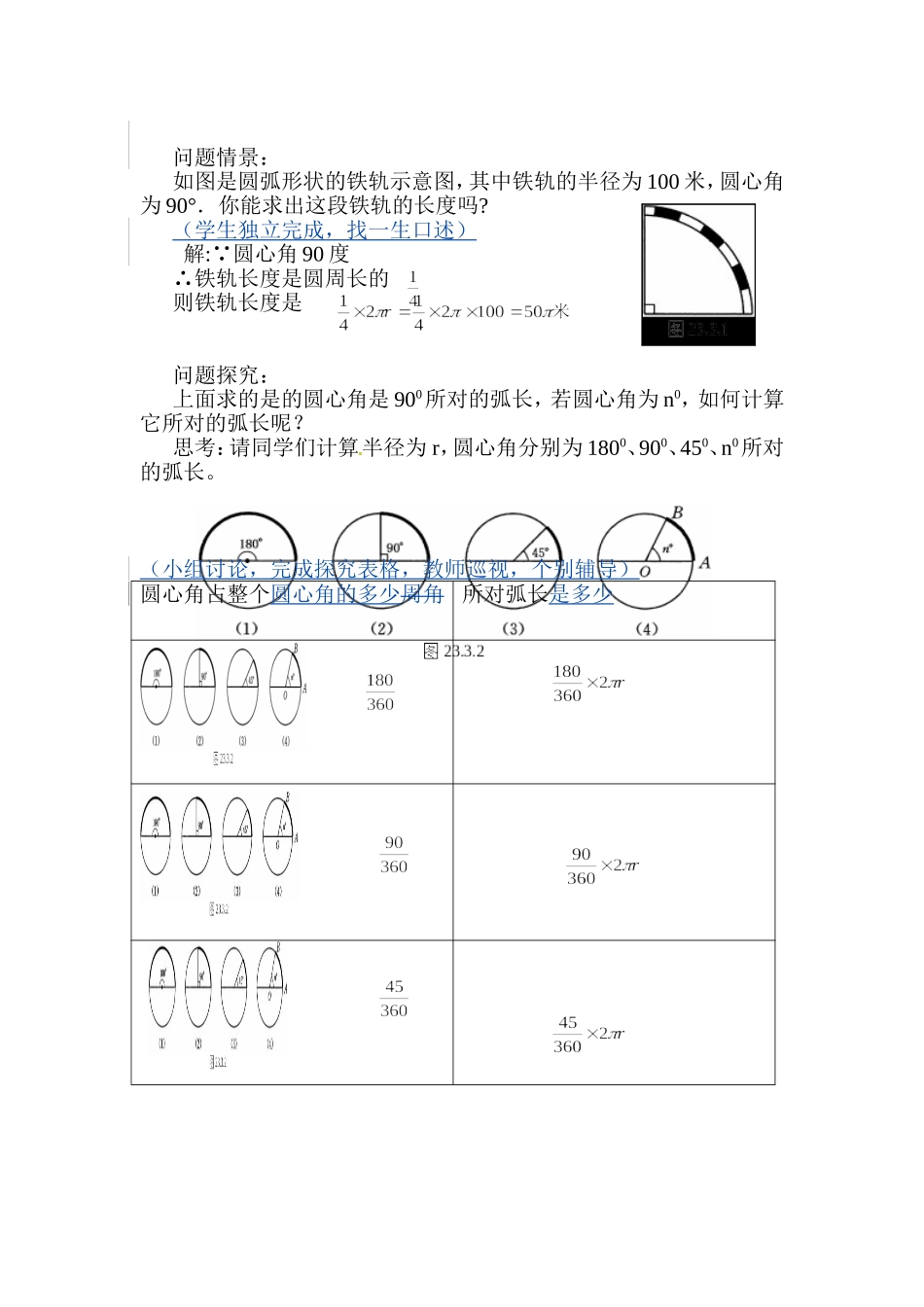
24.4.1弧长和扇形面积一六三中学吴炳桦(第1课时)教学内容1.n°的圆心角所对的弧长L=2.扇形的概念;3.圆心角为n°的扇形面积是S扇形=;4.应用以上内容解决一些具体题目.教学目标了解扇形的概念,理解n°的圆心角所对的弧长和扇形面积的计算公式并熟练掌握它们的应用.通过复习圆的周长、圆的面积公式,探索n°的圆心角所对的弧长L=和扇形面积S扇=的计算公式,并应用这些公式解决一些题目.重难点,关键1.重点:对公式的探索及其它们的应用.2.难点:两个公式的应用.3.关键:由圆的周长和面积迁移到弧长和扇形面积公式的过程。1.重点:由圆的周长和面积迁移到弧长和扇形面积公式的过程.n°的圆心角所对的弧长L=,扇形面积S扇=及其它们的应用.2.难点:两个公式的应用.教具、学具准备圆规、直尺、量角器、圆形纸片课件,探究表格,扇子教学过程一、复习引入(出示课件,一生上板书写)1.圆的周长公式是什么?2.圆的面积公式是什么?二、探索新知(那你会计算吗?)1、把手中的圆形纸片对折,把圆周分成几部分?这几部分什么特征?2、把手中的圆形纸片对折再对折,把圆周分成几部分?这几部分什么特征?3、把手中的圆形纸片对折、对折、再对折,把圆周分成几部分?这几部分什么特征?上述操作中,弧的长度是多少?弧所对的圆心角是多少度?你会求30°圆心角所对的弧的弧长吗?问题情景:如图是圆弧形状的铁轨示意图,其中铁轨的半径为100米,圆心角为90°.你能求出这段铁轨的长度吗?(学生独立完成,找一生口述)解: 圆心角90度∴铁轨长度是圆周长的则铁轨长度是问题探究:上面求的是的圆心角是900所对的弧长,若圆心角为n0,如何计算它所对的弧长呢?思考:请同学们计算半径为r,圆心角分别为1800、900、450、n0所对的弧长。(小组讨论,完成探究表格,教师巡视,个别辅导)圆心角占整个圆心角的多少周角所对弧长是多少ÉÈÐÎÃæ»ýSln¡ãrOQ你能推导出弧长的计算公式吗?(各小组汇报表格)发现结论:如果弧长为,圆心角度数为n,圆的半径为r,那么,弧长的计算公式为:l(公式里哪些是常量,哪些是变量?)练一练:1已知圆弧的半径为50厘米,圆心角为60°,求此圆弧的长度。2已知圆心角为60°,弧长为5π,求圆的半径。扇形:如图,由组成圆心角的两条半径和圆心角所对的弧所围成的图形叫扇形.怎样计算圆心角是n0的扇形面积?圆心角占整个圆心角的多少周角所对扇形面积是多少[来源:学科网ZXXK]你能得出圆心角是n0的扇形的面积公式吗?(各小组汇报完成表格)给出结论:如果弧长为l,圆心角度数为n,圆的半径为r,那么,弧长的计算公式为问:弧长公式和扇形公式有什么联系?扇形的面积等于它的弧长与扇形半径乘积的一半,这与三角形的面积等于底与高乘积的一半很类似。[来源:Z.xx.k.Com](1,2采用口答)练习:1、如果扇形的圆心角是230°,那么这个扇形的面积等于这个扇形所在圆的面积的2、扇形的面积是它所在圆的面积的,这个扇形的圆心角的度数是_________°.3、扇形的面积是S,它的半径是r,这个扇形的弧长是三、例题讲解例:圆心角为的扇形的半径是5cm,求扇形面积和周长。注:要求弧长、扇形面积,都要知道n和R。反之,如果n、R确定,则这个扇形就唯一确定了。例:已知扇形的弧长为cm,圆心角为,则扇形面积是多少?例:已知一个扇形的半径等于一个圆半径的倍,且面积相等,则这个扇形的圆心角等于多少度?例,如图,水平放置的圆柱形排水管道的截面半径是0.6m,其中水面高0.3m,求截面上有水部分的面积(结果保留小数点后两位)解:连接OA、OB,过O作OC⊥AB,垂足为D,交AB于点C,连接AC巩固练习课本P112练习.归纳小结(学生小结,老师点评)作业:教材第115页习题24.4第5题。板书设计24.4.1弧长和扇形面积一复习引入三应用五师生小姐二探索发现例题六作业弧长公式四练习巩固扇形面积公式[课后反思:本节课我采用完全放手让学生用已知的圆周长和圆面积公式来探索新知识弧长和扇形面积,引例的设计主要考虑学生生活实际,学生的心里规律和认识背景,放弃了课本的引例,选择了实际问题,这样能够激发学生的学习欲望,调动学生积极性,让学生积极动手,动...