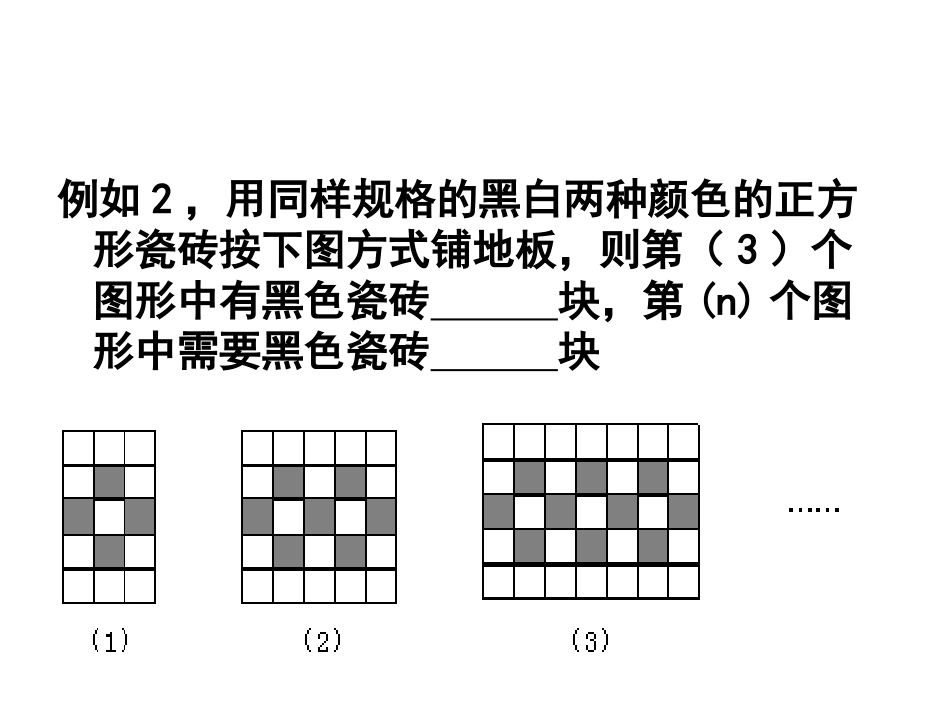
有理数的乘方(3)•例如1、观察下列数表:•根据数列所反映的规律,第n行第n列交叉点上的数应为________.2n-1例如2,用同样规格的黑白两种颜色的正方形瓷砖按下图方式铺地板,则第(3)个图形中有黑色瓷砖块,第(n)个图形中需要黑色瓷砖块1,已知下列等式:①13=12;②13+23=32;③13+23+33=62;④13+23+33+43=102;…………由此规律知,第⑩个等式是.”5522,观察下列各式:0,x,x2,2x3,3x4,5x5,8x6,……。试按此规律写出的第10个式子是。3,观察下列各式数:0,3,8,15,24,……。试按此规律写出的第100个数是_______,第n个数是_______。4、“观察下列球的排列规律(其中●是实心球,○是空心球):●○○●●○○○○○●○○●●○○○○○●○○●●○○○○○●……从第1个球起到第2004个球止,共有实心球_______个34x91002-1n2-16045、观察下列等式填空:10=101、100=102、1000=103、。。。则1000000=10()、若107可表示为__________通过以上例子你发现什么规律?6、比较大小并填空:(1)(-2)2____22、(-2)4___24、(-2)6____26、则(-2)2n___22n(2)(-2)3____-23、(-2)5___-25、(-2)7____-27、则(-2)2n+1___-22n+1========610000000