平行线的性质华师大VIP免费

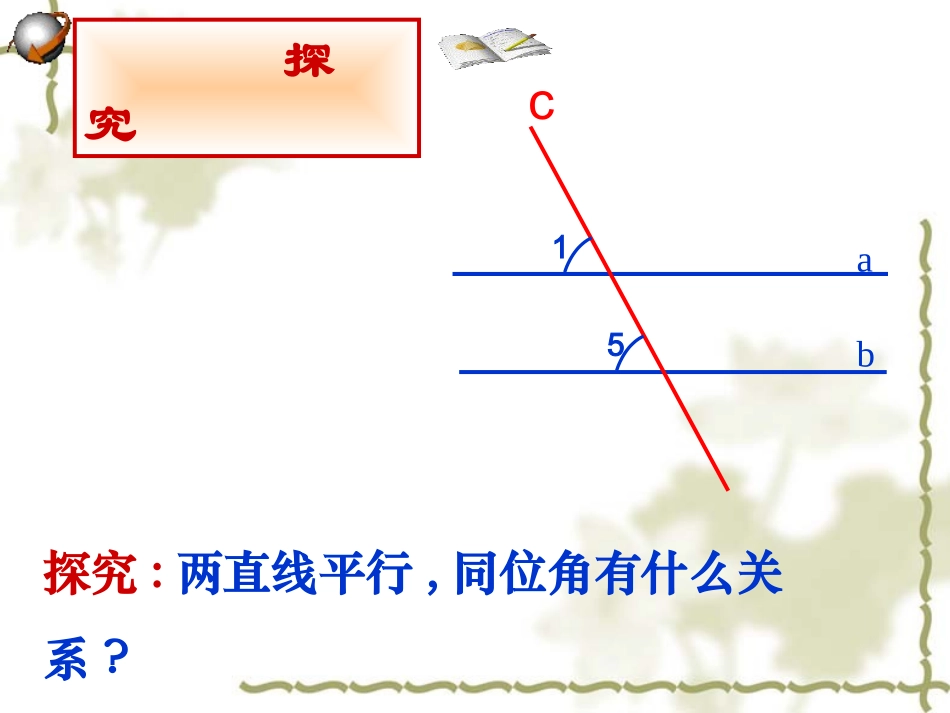
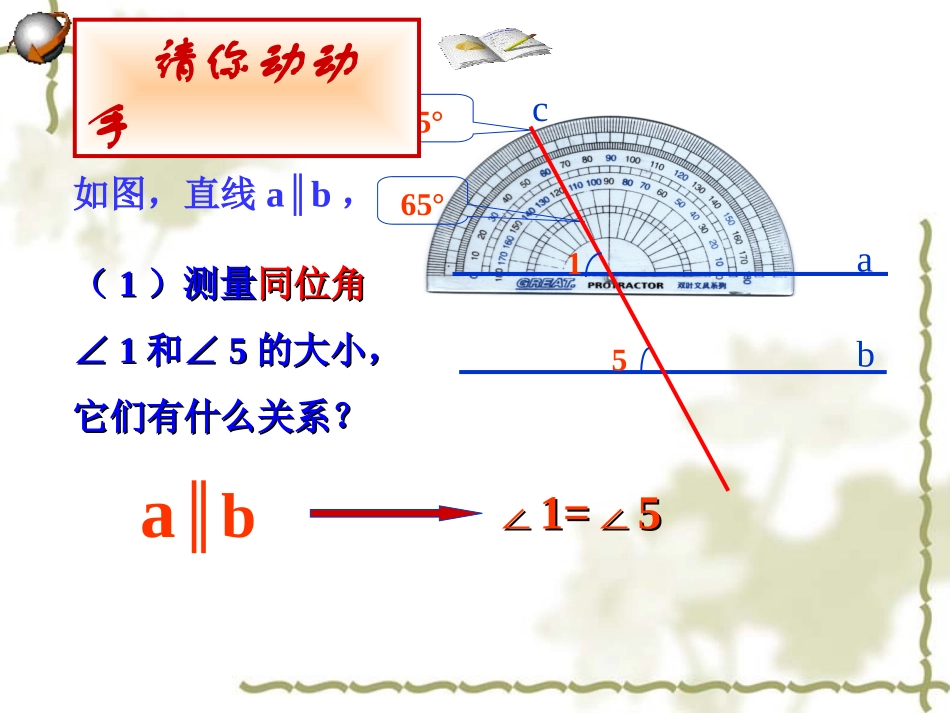
cab15探究探究:两直线平行,同位角有什么关系?如图，直线ab∥，（（11）测量）测量同位角同位角∠∠11和∠和∠55的大小，的大小，它们有什么关系？它们有什么关系？65°65°cab15∠∠1=5∠1=5∠ab∥请你动动手b5ac1∠∠1=5∠1=5∠ab∥请你动动手方法二：裁剪叠合法简简简简简两直线平行，同位角相等．ab12得出结论几何语言表述:∵ab(∥已知)∴∠１＝∠2（两直线平行，同位角相等）两条平行线被第三条直线所截，同位角相等．平行线性质1:如图，已知：a//b,那么3与2有什么关系？我们能否依据“两直线平行，同位角相等”来推理内错角和同旁内角的关系呢？想一想数学语言：如图∵ab∥（已知）∴∠1＝∠2(两直线平行，同位角相等)又∵∠1=3∠（对顶角相等）123ab∴∠2=3∠（等量代换）简简简简简两直线平行，内错角相等．得出结论几何语言表述:∵ab(∥已知)∴∠2＝∠3（两直线平行，内错角相等）两条平行线被第三条直线所截，内错角相等．平行线性质2:123ab简简简简简两直线平行，同旁内角互补．得出结论几何语言表述:∵ab(∥已知)∴∠2+3=180°∠（两直线平行，同旁内角互补）两条平行线被第三条直线所截，同旁内角互补．平行线性质3:c231bac231ba如图：已知a//b，那么2与3有什么关系呢？解：a//b（已知）1=2（两直线平行，同位角相等）1+3=180°（邻补角定义）2+3=180°（等量代换）如图，(1)ab(∵∥已知)∴∠1__2()∠(2)∵a∥b(已知)∴∠2____∠3()(3)∵a∥b(已知)∴∠2＋∠4=____()=两直线平行，同位角相等=两直线平行，内错角相等180°两直线平行，同旁内角互补cab1234书写方法结论结论平行线的性质1（公理）两条平行线平行线被第三条直线所截，同位角相等。简单说成：两直线平行，同位角相等。平行线的性质：性质１：两直线平行，同位角相等．性质２：两直线平行，内错角相等．性质３：两直线平行，同旁内角互补．例1：如图，已知直线ab∥，∠1=50°，求∠2的度数。ab12解：∵ab∥（已知）∴∠2=1∠（两直线平行，内错角相等）∵∠1=50°（已知）∴∠2=50°（等量代换）例2：如图，在四边形ABCD中，ABCD∥，∠B=60°，求∠C的度数.能否求得∠A的度数？ABCD解：∵ABCD∥（已知）∴∠B+C=180°∠（两直线平行，同旁内角互补）∵∠B=60°（已知）∴∠C=180°—B=120°∠（等式的性质）本题中，根据已知条件，无法求出∠A的度数.例如图所示是一块梯形铁片的残余部分，量得∠A=100º，∠B=115°，梯形另外两个角各是多少度？解决问题：1、如图,直线ab,1=54°,2,3,4∥∠∠∠∠各是多少度?解:∵∠2=1(∠对顶角相等)∴∠2=1=54°∠∵ab(∥已知)∴∠4=1=54°(∠两直线平行,同位角相等)∠2+3=180°(∠两直线平行,同旁内角互补)∴∠3=180°－∠2=180°－54°=126°即∠2=54°，∠3=126°，∠4=54°。1234abEDCBA（已知）（1）∵∠ADE=60°B=60°∠∴∠ADE=B∠（等量代换）∴DEBC∥(同位角相等，两直线平行)（2）∵DEBC∥（已证）∴∠AED=C∠(两直线平行，同位角相等)又∵∠AED=40°（已知）（等量代换）∴∠C=40°2、已知∠ADE=60°B=60°AED=40°∠∠证：（１）DEBC∥（２）∠C的度数1、如图，已知平行线AB、CD被直线AE所截(1)从∠1=110o可以知道∠2是多少度?为什么？(2)从∠1=110o可以知道∠3是多少度？为什么？(3)从∠1=110o可以知道∠4是多少度？为什么？一、快速抢答2E134ABDC∠2=110o∵两直线行，内错角相等∠3=110o∵两直线平行,同位角相等∠4=70o∵两直线平行,同旁内角互补一、快速抢答2、如图，一条公路两次拐弯前后两条路互相平行。第一次拐的角∠B是142゜，第二次拐的角∠C是多少度？为什么？ＢＣ∠C=142o∵两直线平行,内错角相等一、快速抢答3、如图直线ab,∥直线b垂直于直线c，则直线a垂直于直线c吗?∟∟abc?ab⊥∵两直线平行,同位角相等同位角相等内错角相等同旁内角互补两直线平行两直线平行判定性质性质已知得到得到已知小结：图形图形已知已知结果结果理由理由同位角同位角内错角内错角同旁内角同旁内角两直线平行同旁内角互补122324））））））abababccc平行线的性质平行线的性质小结小结a//b21两直线平行同位角相等a//b23两直线平行内错角相等a//b)42(18042互补与