南京邮电大学 大学物理 上 §8.4 电势能与电势VIP免费

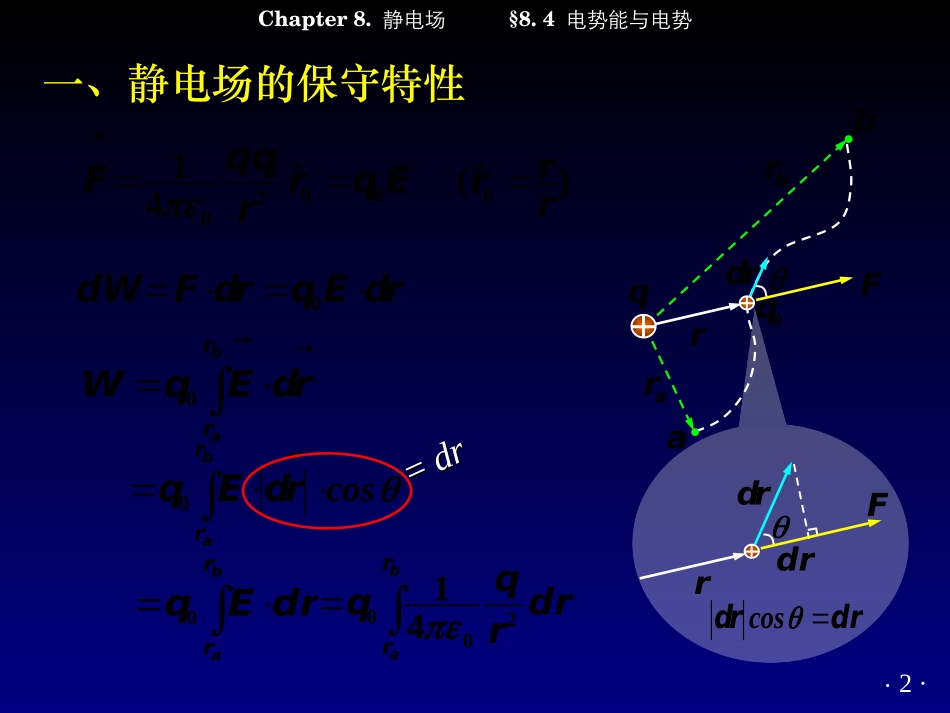
Chapter8.Chapter8.静电场静电场§8.4§8.4电势能与电势电势能与电势·1·§8.4电势能与电势§8.4电势能与电势Chapter8.Chapter8.静电场静电场§8.4§8.4电势能与电势电势能与电势·2·barrdrrqq20041Frrddrdrrdcosarbrab一、静电场的保守特性Frrdq020041rrqqFˆ0qEq0)(0rrrˆrdFdWrdEq0barrrdEqW0barrrdEqcos0==drdrbarrdrEq0Chapter8.Chapter8.静电场静电场§8.4§8.4电势能与电势电势能与电势·3·2L)11(400barrqqW电场力做功只与始末位置有关而电场力做功只与始末位置有关而与中间过程无关，即电场力为保与中间过程无关，即电场力为保守力，静电场为保守力场！守力，静电场为保守力场！2L10LrdEqW20LrdEq01rdErdEL2L2L0LrdE((静电场的静电场的环路定理))ab1L21LLLChapter8.Chapter8.静电场静电场§8.4§8.4电势能与电势电势能与电势·4·二、电势能)11(400barrqqW点电荷点电荷q的电场对点电荷的电场对点电荷q0的作功：的作功：A)abA(A引入点电荷点电荷q0在点电荷在点电荷q电场中的电场中的电势能函数A：：rqqrA004)(一般地，点电荷一般地，点电荷q0在电场在电场E中：中：bardEqW0)abA(AbaAAChapter8.Chapter8.静电场静电场§8.4§8.4电势能与电势电势能与电势·5·babardEqAA0令令::Ab＝0((电势能零点电势能零点))baardEqA0即：点电荷：点电荷q0在电场在电场a点的点的电势能等于将等于将q0从从a点点移移到到b点点((电势能零点电势能零点))电场力所做的功！电场力所做的功！((单位：焦耳单位：焦耳J))☻电势能可电势能可正亦可亦可负，不仅与场源电荷有关，而且与，不仅与场源电荷有关，而且与受力电荷受力电荷q0有关，属于系统，是一种有关，属于系统，是一种相互作用能。。☻电势能电势能A与电势能零点的选取有关，是相对值。与电势能零点的选取有关，是相对值。Chapter8.Chapter8.静电场静电场§8.4§8.4电势能与电势电势能与电势·6·若电荷只集中于某区域，通常选取∞处为势能零点：若电荷只集中于某区域，通常选取∞处为势能零点：0AaardEqA0三、电势baardEqA0baardEqA0比值比值Aa/q0只与分布有关，与只与分布有关，与q0无关无关!!E定义：电势电势baardEV((令令::Vb＝0电势零点电势零点))若令若令::V∞＝0，则：，则：aardEVChapter8.Chapter8.静电场静电场§8.4§8.4电势能与电势电势能与电势·7·☻电势电势V为标量，沿电场方向电势降低。为标量，沿电场方向电势降低。☻若电场分布和电势零点一定，则若电场分布和电势零点一定，则V分布一定；分布一定；V和和一样与受力电荷一样与受力电荷q0无关，都是电场特性描述量。无关，都是电场特性描述量。E☻若为点电荷系，则：若为点电荷系，则：baardEVbaiirdE)(ibairdEiiaV((Via为点电荷为点电荷qi独立存在时在独立存在时在a点产生的电势点产生的电势))即：电势电势V的叠加为标量叠加，而的叠加却为矢量的叠加为标量叠加，而的叠加却为矢量叠加，后者运算较繁。叠加，后者运算较繁。E说明说明Chapter8.Chapter8.静电场静电场§8.4§8.4电势能与电势电势能与电势·8·qV10V8V6等势面分布等势面分布例求点电荷求点电荷q的电势分布。的电势分布。解选∞处为电势零点，则：选∞处为电势零点，则：rrdErV)(☻由于静电场的保守特性，与积分路径无由于静电场的保守特性，与积分路径无关，可选取一合理的路径进行积分。关，可选取一合理的路径进行积分。baardEVrrdrq204rqrV04)(((球对称分布球对称分布))qrraErrdE0cosChapter8.Chapter8.静电场静电场§8.4§8.4电势能与电势电势能与电势·9·课堂练习求半径为求半径为R均匀带电均匀带电Q的球面电势分布。的球面电势分布。解选∞处为电势零点，则：选∞...