矢量旋转变换VIP免费

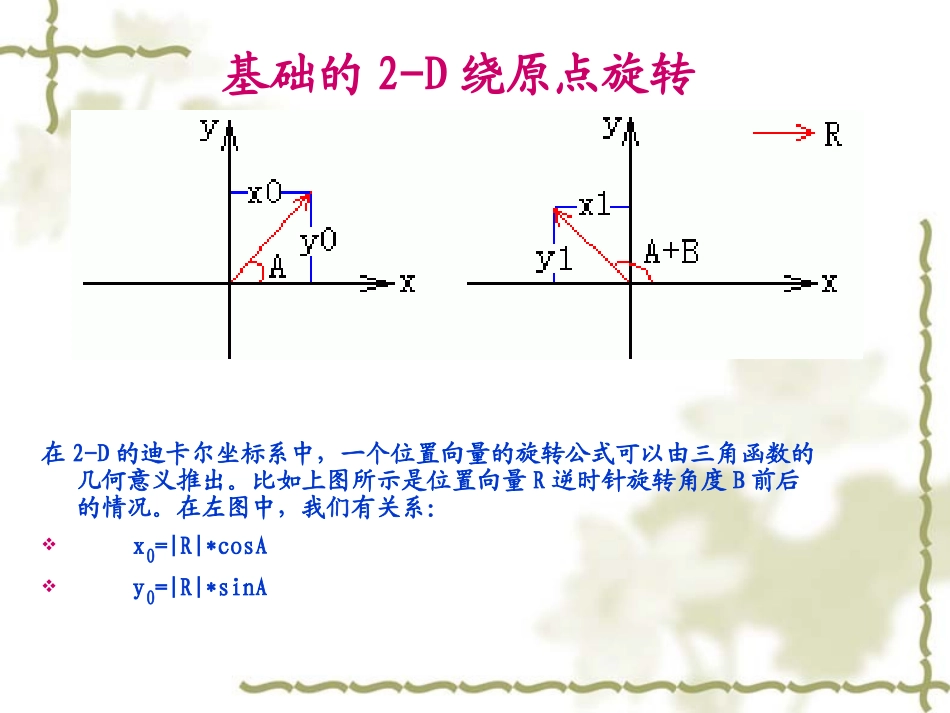
向量的旋转变换西南交通大学基础的2-D绕原点旋转在2-D的迪卡尔坐标系中，一个位置向量的旋转公式可以由三角函数的几何意义推出。比如上图所示是位置向量R逆时针旋转角度B前后的情况。在左图中，我们有关系：x0=|R|*cosAy0=|R|*sinA=>cosA=x0/|R|sinA=y0/|R|下图中，x1=|R|*cos（A+B）y1=|R|*sin（A+B）其中（x1，y1）就是（x0，y0）旋转角B后得到的点，也就是位置向量R最后指向的点。x1=|R|*cos（A+B）y1=|R|*sin（A+B）我们展开cos（A+B）和sin（A+B），得到x1=|R|*（cosAcosB-sinAsinB）y1=|R|*（sinAcosB+cosAsinB）现在把cosA=x0/|R|sinA=y0/|R|代入上面的式子，得到x1=|R|*（x0*cosB/|R|-y0*sinB/|R|）y1=|R|*（y0*cosB/|R|+x0*sinB/|R|）=>x1=x0*cosB-y0*sinBy1=x0*sinB+y0*cosB现在我要把这个旋转公式写成矩阵的形式即：2-D旋转变换矩阵：AsinAcossinAcosAcosAsinAsinAcosA平面旋转矩阵yxvv11cossinsincosyxvv—iR1平移部分平移不是线性的，不能表示为与2×2矩阵相乘的形式。例如要从点(2,1)开始，将其旋转90度，在x方向将其平移3个单位，在y方向将其平移4个单位。可通过先使用矩阵乘法再使用矩阵加法来完成此操作。111BPRBPiii111OPOBROPOBiii1111OPROPOBROBiiii∴θiP1B1θ10xyPiBi111111111111cossinsincoscossinsincosPPiiiiPiPiBBiiiiBiBiyxyxyxyxiPiPPiiBiBiPiPPiiBiBBiBiyxyyxyxxyxyx1111111111111111cossincossinsincossincos补充部分平移部分平移不是线性的，不能表示为与2×2矩阵相乘的形式。例如要从点(2,1)开始，将其旋转90度，在x方向将其平移3个单位，在y方向将其平移4个单位。可通过先使用矩阵乘法再使用矩阵加法来完成此操作。后面跟一平移（与1×2矩阵相加）的线性变换（与2×2矩阵相乘）称为仿射变换。放射变换（先乘后加）可以通过乘以一个3*3的矩阵来实现，若要使其起作用，平面上的点必须存储于具有虚拟第三坐标的1×3矩阵中。通常的方法是使所有的第三坐标等于1。例如，矩阵[211]代表点(2,1)。例如与单个3×3矩阵相乘的仿射变换（旋转90度；在x方向上平移3个单位，在y方向上平移4个单位）：在前面的示例中，点(2,1)映射到了点(2,6)。其中3×3矩阵的第三列包含数字0，0，1。对于仿射变换的3×3矩阵都是这样的。重要的数字是列1和列2中的6个数字。矩阵左上角的2×2部分表示变换的线性部分，第3行中的前两项表示平移。在使用3*3的矩阵做仿射变换时候，表示点的矩阵变成了一个1*3矩阵，这个矩阵中的最后一个值必须设置成1。对于3*3矩阵，其最后一列的值是多少是没有关系的，因为他们不会影响结果中的前两列。不过如上，经常将他们设置为0，0，1。这一列对于坐标转换的结果并没有任何影响，但是他们是必须的，因为矩阵相乘必须满足“相乘的两个矩阵第一个矩阵的列数必须与第二个矩阵的行数相同”。平面或空间里的每个线性变换（这里就是旋转变换）都对应一个矩阵，叫做变换矩阵。对一个点实施线性变换就是通过乘上该线性变换的矩阵完成的。把顶点和矩阵相乘，就会发现矩阵的某些项，扮演着为顶点变换（平移、旋转、缩放）提供参数的作用。（前人总结出来，填哪些那些项能得到平移矩阵/缩放矩阵/旋转矩阵）比如平移矩阵，你自己拿一个顶点和它相乘，算一遍，就会发现它化简到最后一步时的算式，和顶点平移算式是一样的。旋转、缩放也是如此。那么为什么还要和矩阵相乘？直接用平移算式、旋转算式、缩放算式不就行了？不行因为靠矩阵来计算可以减少计算量。一个顶点要进行多次变换，比如平移后旋转再平移之后再缩放，用简单算式得算4遍，矩阵只要算一遍。原理就是公式：（顶点×矩阵A）×矩阵B=顶点×（矩阵A×矩阵B），即矩阵接合律的推广。（矩阵一般不遵守分配律，所以顶点变换有先后顺序...