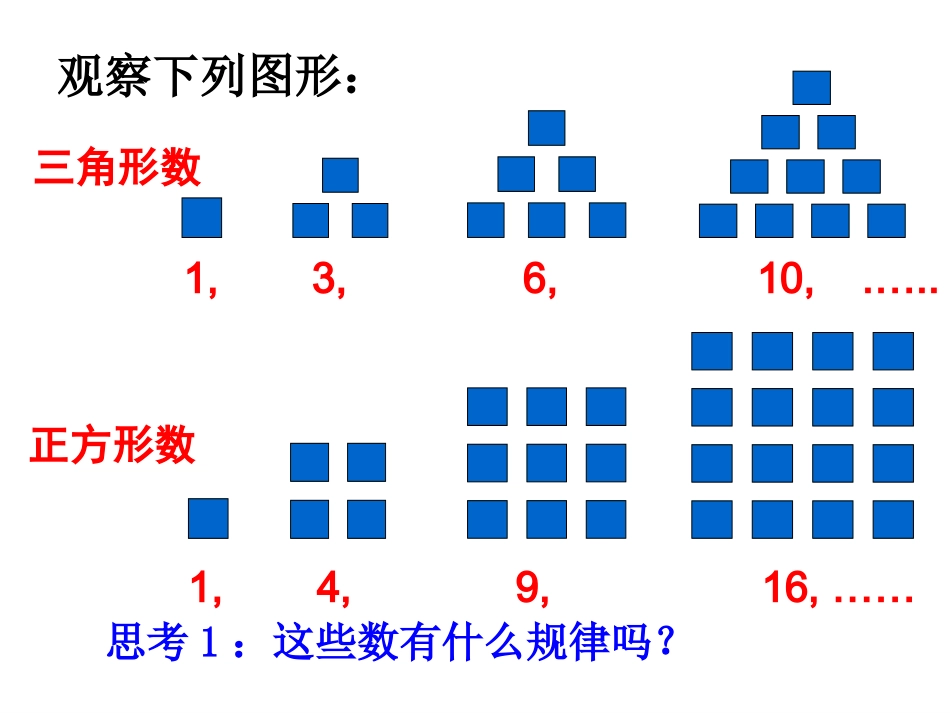
三角形数1,3,6,10,.…..正方形数1,4,9,16,……观察下列图形:思考1:这些数有什么规律吗?1,2,3,4,5,···n,···.(1)1,,,,,···,···.(2)n1213141511,1.4,1.41,1.414,···.(3)-1,1,-1,1,···.(5)10,9,8,7,6,5,4.(4)3,3,3,3.(6)思考2:这些数的共同特点是什么?按照一定顺序排列的一列数按照一定顺序排列的一列数叫数列。按照一定顺序排列的一列数叫数列。数列中的每一个数叫做这个数列的项。数列中的每一项都和它的序号有关,排第一位的数称为这个数列的第1项(首项),排第二位的数称为这个数列的第2项,······,排第n位的数称为这个数列的第n项.1、数列定义2、数列的项:如:数列(4)10,9,8,7,6,5,4。数列(4′)4,5,6,7,8,9,10。如:数列(5)-1,1,-1,1,···。1.相同的一组数按不同的顺序排列时,是否为同一数列?2.一个数列的数可以重复吗?3、数列的一般形式a1,a2,a3,…an,…上面数列可简记为{an},其中an是数列的第n项2)根据数列项的大小分:递增数列:从第2项起,每一项都大于它的前一项的数列递减数列:从第2项起,每一项都小于它的前一项的数列常数数列:各项相等的数列。摆动数列:从第2项起,有些项大于它的前一项,有些项小于它的前一项的数列有穷数列:项数有限的数列.例如数列1,2,3,4,5,6。是有穷数列无穷数列:项数无限的数列.例如数列1,2,3,4,5,6,…是无穷数列1)根据数列项数的多少分:1nnaa()1nnaa()1nnaa()4、数列的分类练习P28观察这说明:数列的项an是序号n的函数.所以:数列可以看成以正整数集N*(或它的有限子集{1,2,3,4,…,n})为定义域的函数an=f(n),当自变量按照从小到大的顺序依次取值时,所对应的一列函数值。反过来,对于函数y=f(x),如果f(i)(i=1,2,3,…)有意义,那可得到一个数列f(1),f(2),f(3),…f(n),…即数列是一种特殊的函数。,,,,,51413121112345…项an序号n5、数列与函数的关系6、数列的通项公式如果数列{an}的第n项与n之间的关系可以用一个公式来表示,那么这个公式就叫做这个数列的通项公式。1nan1nna()1,,,,,···.21314151如数列:通项公式为又如数列:-1,1,-1,1,···.通项公式为(1)(2)1nnannann1na根据下面数列的通项公式,写出它的前4项:关于数列的通项公式3、数列的通项公式不一定是一个式子,也可以是分段函数.1、不是每一个数列都能写出其通项公式(如数列5)1,1.4,1.41,1.414,…2、数列的通项公式不唯一如:1,1,1,1,…可写成(1)nna121,12,nnkkNankkN或4、数列通项公式的作用:①求数列中任意一项;②检验某数是否是该数列中的一项。例1、写出下面数列的一个通项公式,使它的前4项分别是下列各数:12,4,6,8;2491625111(3)123442020()(),,,;,,,;(),,,。练习:P311,42nan2)1(nan11(1)nnan1)1(1nna观察数列通项公式的关键是探求第n项an与项数n的关系数列2,4,6,8,10,……其通项公式是:nan2图象为:an1098765432012345nnan122436…………k2k列表为:图象为直线上的无数个孤立点例2、图中的三角形称为谢宾斯基(Sierpinski)三角形,在下图4个三角形中,着色三角形的个数依次构成一个数列的前4项,请写出这个数列的一个通项公式,并在直角坐标系中画出它的图象。an30272421181512963o12345n13nna图象为曲线上的无数个孤立点1,3,6,10,.…..提问:这些数有什么规律吗?首项为1,从第2项起,第n项等于第n-1项加上n.也就是a1=1,an=an-1+n(n>1)已知数列{an}的首项(或前几项),且任一项an与它的前一项an-1(或前几项)间的关系可用一个式子来表示,那么这个式子就叫做这个数列的递推公式。递推公式也是数列的一种表示方法。7、数列的递推公式如数列1,3,6,10的递推公式可表示为a1=1,an=an-1+n(n>1)解析式法列表法图象法1.通项公式2.递推公式一群孤立的点8、数列的表示方法例3、设数列满足写出这个数列的前5项。na111111naaann解:由题意可知58113...