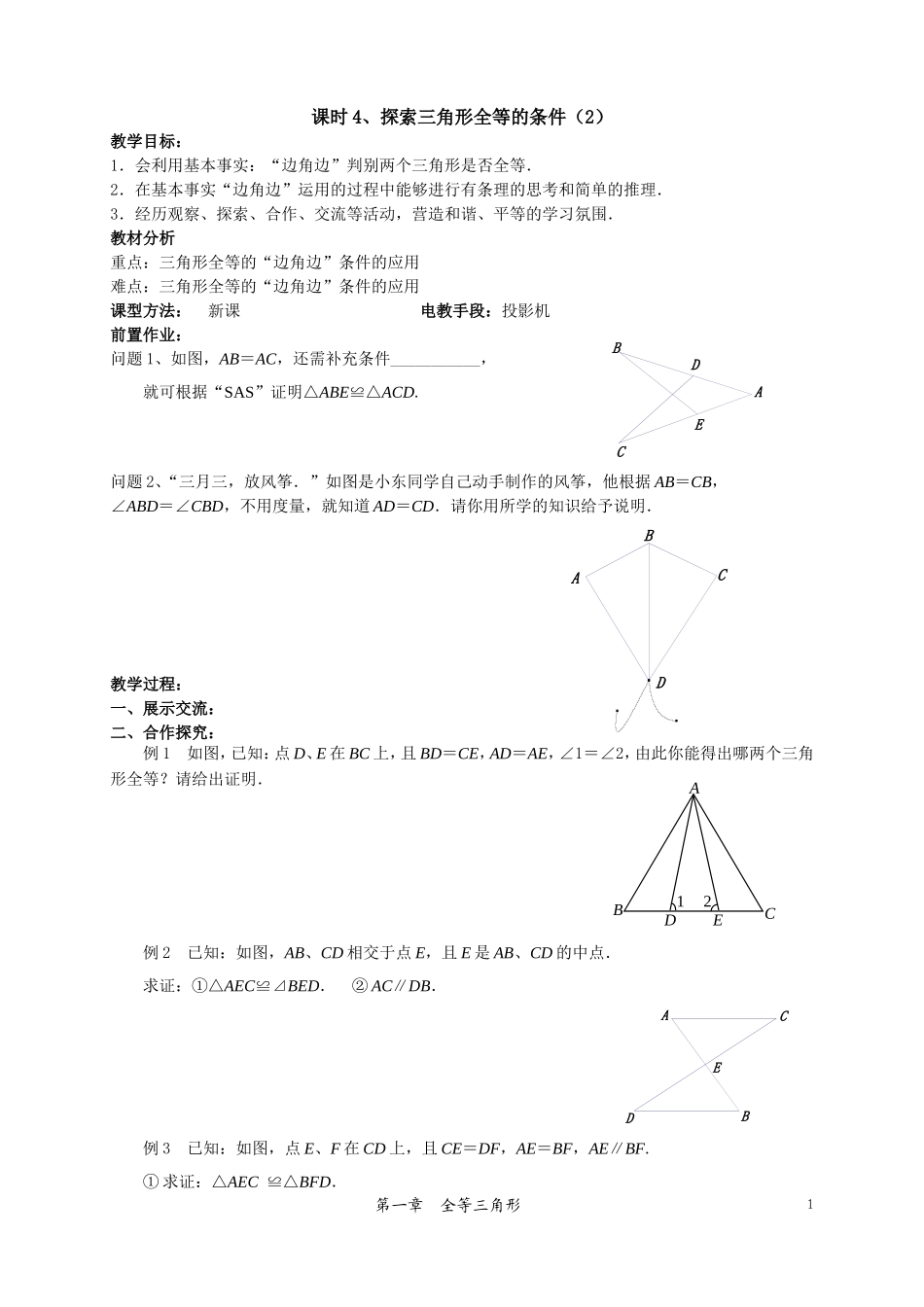
课时4、探索三角形全等的条件(2)教学目标:1.会利用基本事实:“边角边”判别两个三角形是否全等.2.在基本事实“边角边”运用的过程中能够进行有条理的思考和简单的推理.3.经历观察、探索、合作、交流等活动,营造和谐、平等的学习氛围.教材分析重点:三角形全等的“边角边”条件的应用难点:三角形全等的“边角边”条件的应用课型方法:新课电教手段:投影机前置作业:问题1、如图,AB=AC,还需补充条件___________,就可根据“SAS”证明△ABE≌△ACD.问题2、“三月三,放风筝.”如图是小东同学自己动手制作的风筝,他根据AB=CB,∠ABD=∠CBD,不用度量,就知道AD=CD.请你用所学的知识给予说明.教学过程:一、展示交流:二、合作探究:例1如图,已知:点D、E在BC上,且BD=CE,AD=AE,∠1=∠2,由此你能得出哪两个三角形全等?请给出证明.例2已知:如图,AB、CD相交于点E,且E是AB、CD的中点.求证:①△AEC≌⊿BED.②AC∥DB.例3已知:如图,点E、F在CD上,且CE=DF,AE=BF,AE∥BF.①求证:△AEC≌△BFD.第一章全等三角形1EBDCADCBAABDEC12CBADE②你还能证得其他新的结论吗?③本例图中的△AEC可以通过_________变换得到例2所示图形.三、质疑反馈1、已知:如图,C是AB的中点,AE=BD,∠A=∠B.求证:∠E=∠D.2、已知:如图,点D在AE上,BD=CD,∠BDE=∠CDE.求证:AB=AC3、已知:如图,AB∥CD,AB=CD.求证:AD∥BC.第一章全等三角形2FCBADEEDCBAEDCBADCBA