1.2.1平面的基本性质(1)VIP免费

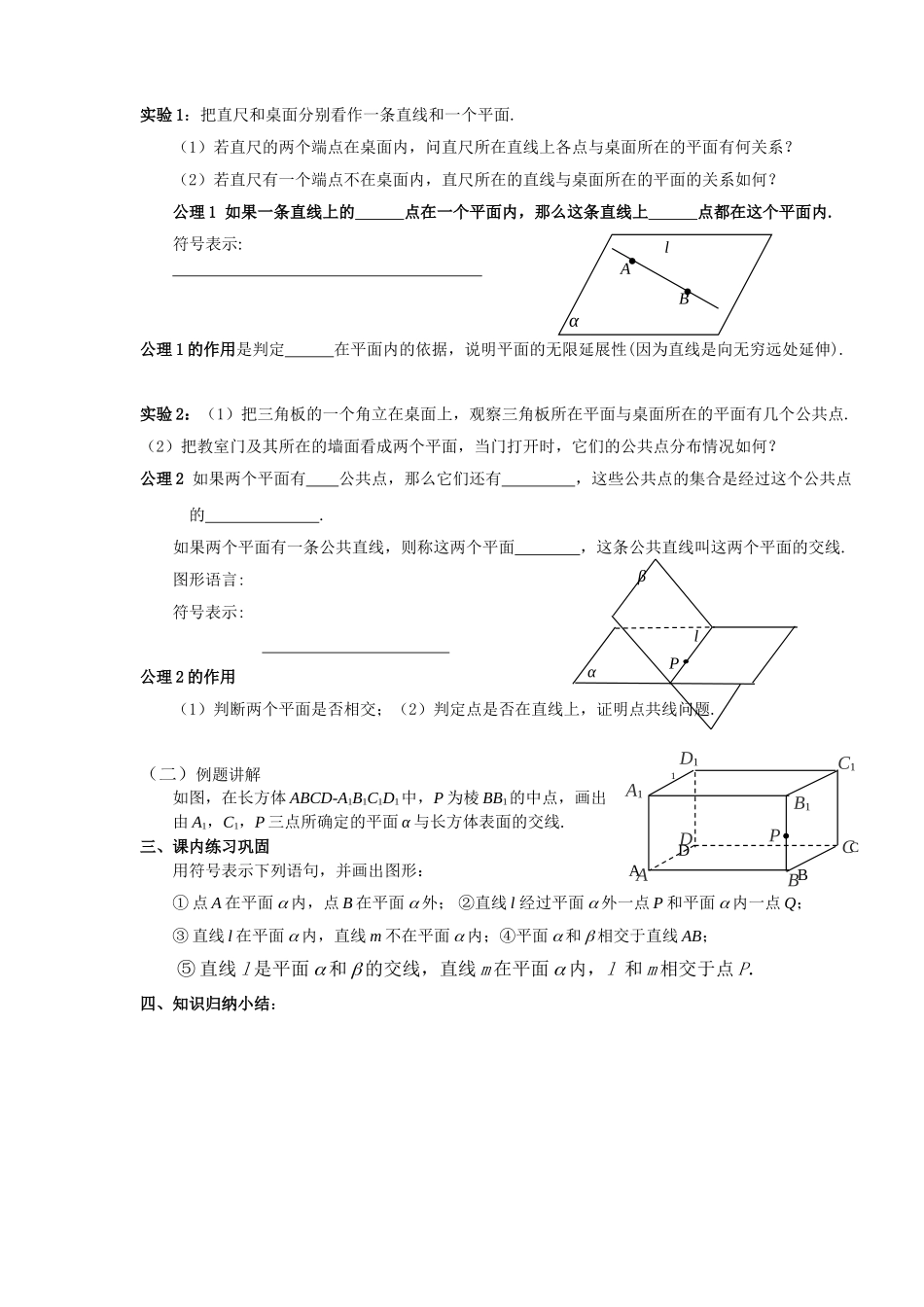
1.2.1平面的基本性质（1）【学习目标】1.初步理解平面的概念；了解平面的基本性质（公理1、2）；2.能正确使用集合符号表示有关点、线、面的位置关系；【学习重点】平面的基本性质．【学习难点】正确使用图形语言、符号语言表示平面的基本性质.【教学过程】一、课前预习导学：（一）问题情境立体几何平面几何现实生活中有哪些事物能够给我们以平面的形象，它们的共同特征主要有哪些？（二）引入课题思考、联想列举出诸如平静的水面、广阔的平原、光滑的桌面、黑板面等等平面的形象．进而归纳出它们的共同特征是平坦的、与厚薄（有、无）关．（三）建构数学1．平面的认识（无限延展的、没有厚薄）；2．平面的表示；(1)图形语言通常用形表示平面(2)符号语言通常用希腊字母α、β、γ等来表示，也可以用来表示，如平面α、平面AC等3.点、直线、平面之间的基本关系点P在直线AB上，记作点C不在直线AB上，记作点M在平面AC内，记作点A1不在平面AC内，记作；直线AB与直线BC交于点B，记作；直线AB在平面AC内，记作直线AA1不在平面AC内，记作（四）解决问题（1）下列叙述中，正确的是_______①因为Pα，Qα，所以PQα；②因为Pα，Q，所以α∩＝PQ；③因为ABα，CAB，DAB，所以CDα；④因为ABα，ABβ，所以∩＝AB.二、课堂学习研讨（一）汇报交流平面的基本性质；投影实验1：把直尺和桌面分别看作一条直线和一个平面.（1）若直尺的两个端点在桌面内，问直尺所在直线上各点与桌面所在的平面有何关系？（2）若直尺有一个端点不在桌面内，直尺所在的直线与桌面所在的平面的关系如何？公理1如果一条直线上的点在一个平面内，那么这条直线上点都在这个平面内.符号表示:公理1的作用是判定在平面内的依据，说明平面的无限延展性(因为直线是向无穷远处延伸).实验2：（1）把三角板的一个角立在桌面上，观察三角板所在平面与桌面所在的平面有几个公共点.（2）把教室门及其所在的墙面看成两个平面，当门打开时，它们的公共点分布情况如何？公理2如果两个平面有公共点，那么它们还有，这些公共点的集合是经过这个公共点的.如果两个平面有一条公共直线，则称这两个平面，这条公共直线叫这两个平面的交线.图形语言:符号表示:公理2的作用（1）判断两个平面是否相交；（2）判定点是否在直线上，证明点共线问题.（二）例题讲解如图，在长方体ABCD-A1B1C1D1中，P为棱BB1的中点，画出由A1，C1，P三点所确定的平面α与长方体表面的交线.三、课内练习巩固用符号表示下列语句，并画出图形：①点A在平面内，点B在平面外；②直线l经过平面外一点P和平面内一点Q；③直线l在平面内，直线m不在平面内；④平面和相交于直线AB；⑤直线l是平面和的交线，直线m在平面内，l和m相交于点P．四、知识归纳小结：αβlPABCD1A1C1B1D1ABCDPαABl