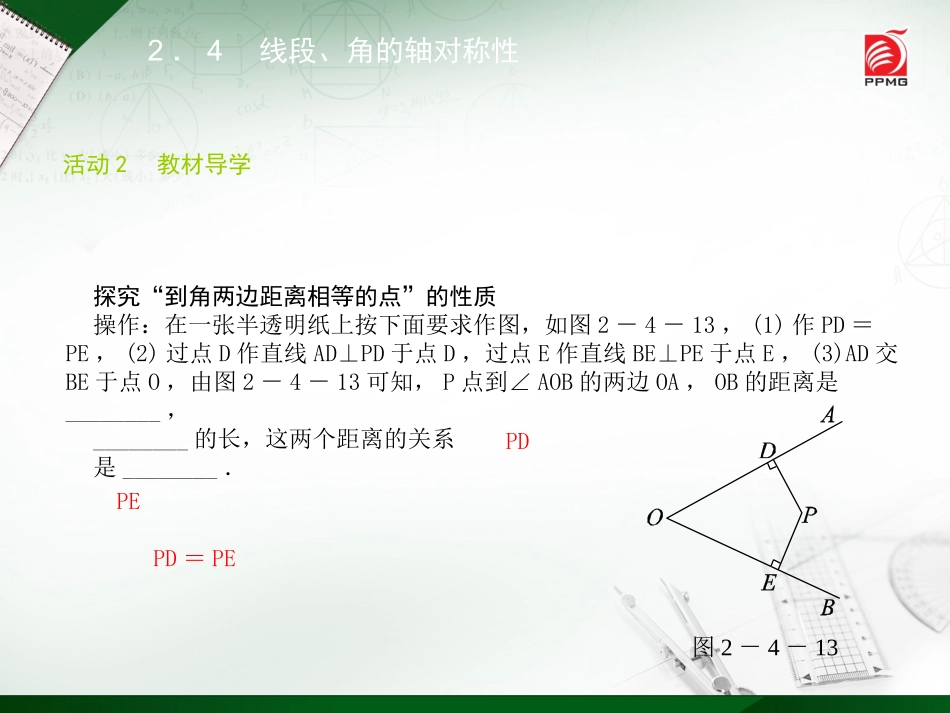
2.3线段、角的对称性(3)八年级(上册)初中数学探究新知2.4线段、角的轴对称性活动1知识准备如图2-4-5,若OC平分∠AOB,∠AOB=60°,则∠AOC=________°.图2-4-5302.4线段、角的轴对称性活动2教材导学探究“到角两边距离相等的点”的性质操作:在一张半透明纸上按下面要求作图,如图2-4-13,(1)作PD=PE,(2)过点D作直线AD⊥PD于点D,过点E作直线BE⊥PE于点E,(3)AD交BE于点O,由图2-4-13可知,P点到∠AOB的两边OA,OB的距离是________,________的长,这两个距离的关系是________.图2-4-13PDPEPD=PE2.4线段、角的轴对称性◆知识链接——[新知梳理]知识点二验证:连接OP,沿OP折叠,观察OP是否为∠AOB的平分线.证明:你能用学过的知识证明发现的结论吗?[答案]验证:OP是∠AOB的平分线证明:连接OP,∵AD⊥PD,BE⊥PE,∴∠PDO=∠PDO=90°.又∵PD=PE,OP=OP,∴△PDO≌△PEO(HL),∴∠POD=∠POE,∴OP是∠AOB的平分线.新知梳理2.4线段、角的轴对称性知识点一角平分线的性质角的轴对称性:角是________图形,______________________是它的对称轴.角平分线的性质:角平分线上的点到角两边的距离________.轴对称角平分线所在的直线相等2.4线段、角的轴对称性[注意](1)角平分线不能视为角的对称轴(角平分线是一条射线,因此只能视为角的对称轴的一部分).(2)角平分线性质的应用格式:如图2-4-14,∵OP平分∠AOB,PM⊥OA,PN⊥OB,∴PM=PN.其中两个垂直是不可缺少的条件.图2-4-142.4线段、角的轴对称性知识点二角平分线的判定角的内部到角两边距离相等的点在角的________上.平分线[注意](1)角平分线是到角两边距离相等的点的集合.(2)应用格式:如图2-4-15,∵PM⊥OA,PN⊥OB,PM=PN,∴OP平分∠AOB.其中两个垂直是不可缺少的条件.图2-4-15重难题型探究2.4线段、角的轴对称性题型一利用角平分线的性质解决问题例1[教材补充例题]如图2-4-7,在△ABC中,∠C=90°,AC=BC,AD平分∠BAC,DE⊥AB于点E.若AB=10,求△BDE的周长.图2-4-72.4线段、角的轴对称性[解析]由已知条件知CD=ED,所以ED+BD+BE=BC+BE.又因为BC=AC,由△ACD≌△AED,得AC=AE,所以△BDE的周长为AE+BE=AB=10.2.4线段、角的轴对称性解:因为AD平分∠BAC,DE⊥AB,CD⊥AC,所以CD=ED.又因为AD=AD,所以Rt△ACD≌Rt△AED,所以AC=AE.又因为AC=BC,所以BC=AE,所以△BDE的周长=ED+BD+BE=AE+BE=AB=10.2.4线段、角的轴对称性[归纳总结]利用角平分线的性质,可以推出图形中相等的线段,利用相等线段可以构建全等三角形.问题中若有角平分线,可利用角平分线的性质寻找相等的角或相等的线段来解决问题.2.4线段、角的轴对称性题型二利用角平分线解决实际问题例2[迁移运用题]如图2-4-8,两条直线AB,CD相交于点O,点M在OD上,在∠AOD的内部有一点N,现要在∠AOD内部找一个点P,使点P到AB,CD的距离相等,且使PM=PN,用尺规作出点P的位置.(不写作法,保留作图痕迹)图2-4-82.4线段、角的轴对称性[解析]要找一个到AB,CD的距离相等的点,可以知道它一定在∠AOD的平分线上,同时点P还满足PM=PN,所以它一定在点M,N连线的垂直平分线上.因此,点P必在角平分线与垂直平分线的交点上.解:如图2-4-3所示,点P即为所求.图2-4-32.4线段、角的轴对称性[归纳总结]本题要求能够根据线段垂直平分线和角平分线的性质,探求点P所在的位置.在实际问题中,有时需要确定到线段或点距离相等的点的位置.除了垂直平分线的性质能够提供线段相等外,角平分线的性质也能提供线段相等,因此就可以利用尺规作图来解决这样的问题.课堂总结反思2.4线段、角的轴对称性相等相等轴对称角平分线所在的直线2.4线段、角的轴对称性[反思]角平分线是角的对称轴,这种说法是否正确,若不正确,请说明理由,并改正.[答案]不正确,因为角平分线是射线,对称轴是直线.应改为角平分线所在的直线是角的对称轴.