直线与圆的位置关系VIP免费

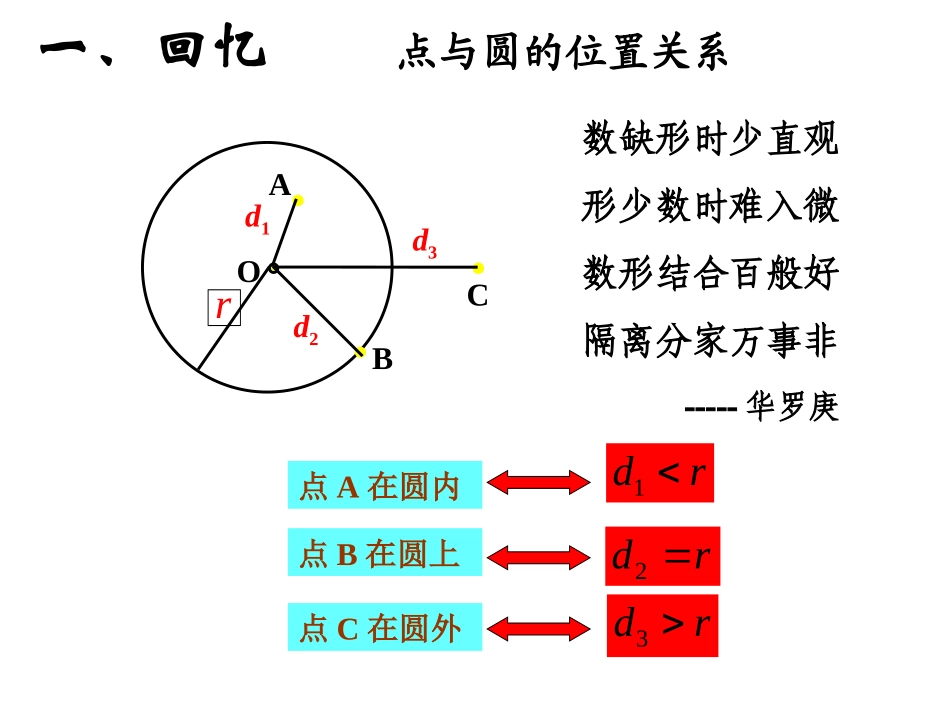
海口市灵山中学杨克丹（一）学习目标•1、了解直线与圆的三种位置关系，理解直线与圆相离、相切、相交的概念；•2、从运动的观点及量变到质变的观点来理解直线与圆的三种位置关系和相离、相切、相交的概念。（二）重点、难点•1、用数量关系（圆心到直线的距离）判断直线与圆的位置关系；•2、灵活运用直线与圆的位置关系。一、回忆点与圆的位置关系O点B在圆上点A在圆内rd2rd1点C在圆外rd3ABCd1d2d3r数缺形时少直观形少数时难入微数形结合百般好隔离分家万事非-----华罗庚如果把点换成一条直线，直线和圆又有哪几种位置关系？课题：§27.2.2直线与圆的位置关系二、新授●O●O把太阳看成一个圆，地平线看成一条直线,注意观察直线与圆的公共点的个数a(地平线)a(地平线)●O●O●O三•你发现这个自然现象反映出直线和圆的公共点个数有种情况●●●●•把钥匙环看作一个圆,把直尺边缘看成一条直线.•固定圆,平移直尺,直线和圆分别有几个公共点?●O●O相交●O相切相离直线与圆的公共点个数可判定它们的位置关系。直线和圆只有一个公共点,这时我们就说这条直线和圆相切,这条直线叫做圆的切线,这个点叫做切点.直线和圆有两个公共点,这时我们就说这条直线和圆相交,这条直线叫做圆的割线直线和圆没有公共点,这时我们就说这条直线和圆相离.两个公共点没有公共点一个公共点1.直线和圆的位置关系有三种(从直线与圆公共点的个数)2.用图形表示如下:.o.oll相切相交切线切点割线...没有公共点有一个公共点有两个公共点.ol相离交点快速判断下图中直线L与⊙O的位置关系（1）（2）（3）（4）（5）相离相切相交相交？LLLLL·O·O·O·O·O(从直线与圆公共点的个数)？L如果公共点的个数不好判断，我们该怎么办？·O·A·B能否用数量关系来体现直线与圆的位置关系？•如图,圆心O到直线的距离d与⊙O的半径r的大小有什么关系?●O●O相交●O相切相离直线与圆的位置关系量化rrr┐dd┐d┐1)直线和圆相交dr;dr;2)直线和圆相切3)直线和圆相离dr;<=>1)直线和圆相交dr;dr;2)直线和圆相切3)直线和圆相离dr;直线与圆的位置关系量化●O●O相交●O相切相离rrr┐dd┐d┐<=>你能根据d与r的大小关系确定直线与圆的位置关系吗?小结：直线与圆的位置关系：0d>r1d=r切点切线2d6cmd=6cmd<6cm0cm≤2.2.直线和圆有直线和圆有22个交点个交点,,则直线和圆则直线和圆_________________;_;直线和圆有直线和圆有11个交点个交点,,则直线和圆则直线和圆________________;__;直线和圆有没有交点直线和圆有没有交点,,则直线和圆则直线和圆________________;__;相交相交相切相切相离相离三、习题巩固：已知圆的半径为6.5cm，如果圆心到直线的距离为:（1）d=4.5cm时，直线与圆的位置关系是，有个公共点；（2）d=6.5cm时，直线与圆的位置关系是，有个公共点；（3）d=8cm时，直线与圆的位置关系是，有个公共点。3、6.54.58相交相切相离210直134、O的半径为３ｃｍ，点Ｐ在直线L上，若ＯＰ＝３ｃｍ，则O与L的关系是（）Ａ．相交Ｂ．相切Ｃ．相离Ｄ．相交或相切火眼金睛5、在RtABC△中，∠C=90°，AC=3cm,BC=4cm,以C为圆心，r为半径的圆与AB有怎样的关系？（1）r=2cm;（2）r=2.4cm;（3）r=3cm.BCAD解：过点C作CD⊥AB于点D，在Rt△ABC中,根据三角形面积公式有即圆心C到AB的距离d=2.4cm.（1）当r=2cm时，有d>r，因此⊙O和AB相离.（2）当r=2.4cm时，有d=r，因此⊙O和AB相切.（3）当r=3cm时，有d