14.2勾股定理的应用VIP免费

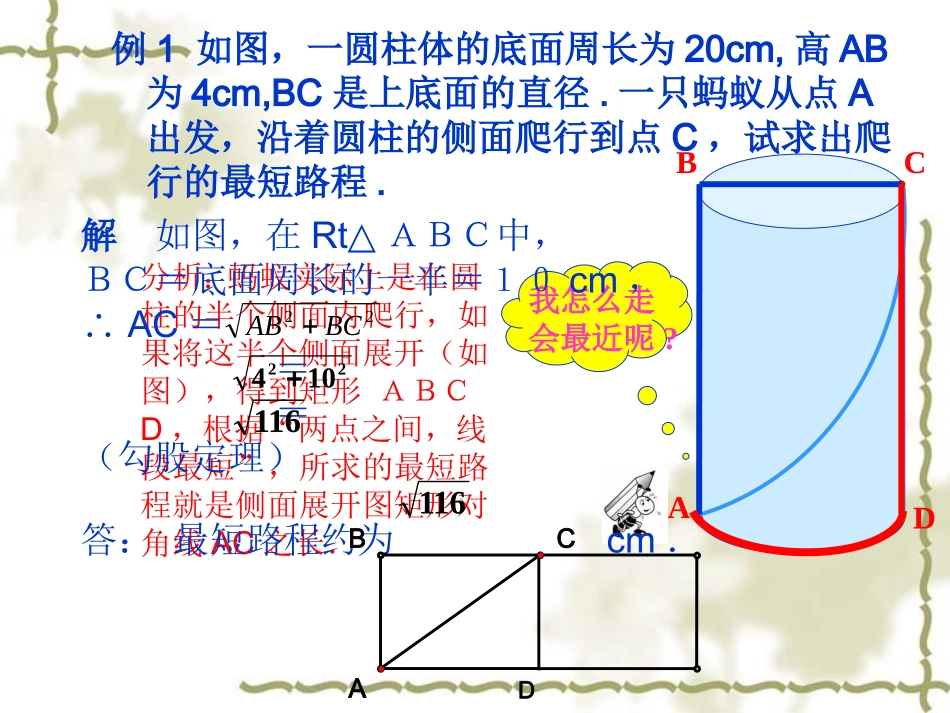
天水市七中授课教师：何旭东指导老师：陈秀琴华东师大版数学八年级上册如果三角形的三条边长分别是a,b,c，满足那么这个三角形是直角三角形a2+b2=c2勾股定理的逆定理如果直角三角形的两条直角边分别是a,b,斜边为c,那么a2+b2=c2互为逆定理勾股定理例1如图，一圆柱体的底面周长为20cm,高AB为4cm,BC是上底面的直径.一只蚂蚁从点A出发，沿着圆柱的侧面爬行到点C，试求出爬行的最短路程.ABCD我怎么走会最近呢?分析：蚂蚁实际上是在圆柱的半个侧面内爬行，如果将这半个侧面展开（如图），得到矩形ＡＢＣD，根据“两点之间，线段最短”，所求的最短路程就是侧面展开图矩形对角线AC之长．解如图，在Rt△ＡＢＣ中，ＢＣ＝底面周长的一半＝１０cm，∴AC＝＝＝（勾股定理）答：最短路程约为cm．22BCAB22104116ACBD116拓展1如果圆柱换成如图的棱长为10cm的正方体盒子，蚂蚁沿着表面需要爬行的最短路程又是多少呢？ABAB101010BCA101010CBA例2一辆装满货物的卡车，其外形高2.5米，宽1.6米，要开进厂门形状如图的某工厂，问这辆卡车能否通过该工厂的厂门?说明理由。ABMNOC┏DH2米2.3米分析：由于厂门宽度足够,所以卡车能否通过,只要看当卡车位于厂门正中间时其高度是否小于CH．如图所示,点D在离厂门中线0.8米处,且CDAB,⊥与地面交于H．解：CD＝22ODOC228.01CH＝0.6＋2.3＝2.9(米)＞2.5(米).因此高度上有0.4米的余量，所以卡车能通过厂门．在RtOCD△中，由勾股定理得＝＝0.6米，例3葭生池中今有方池一丈，葭生其中央，出水一尺，引葭赴岸，适与岸齐。问：水深、葭长各几何？解：可设葭长为x尺，则水深为(x-1)尺则有:(x-1)2+52=x2解得：x=13所以：葭长13尺，水深12尺。5尺水池1尺X-1尺X尺练习1.如图,从电杆离地面5米处向地面拉一条长7米的钢缆，求地面钢缆固定点A到电杆底部B的距离.C解：如图，在Rt△ＡＢＣ中，AC=7米，BC=5米，24572222BCACAB答：地面钢缆固定点A到电杆底部B的距离是米.（米）24由勾股定理，得练习2.如图所示，校园内有两棵树相距12米，一棵树高13米，另一棵树高8米，一只小鸟从一棵树的顶端飞到另一棵树的顶端，小鸟至少要飞米.13米12米8米ABC13拓展2如果盒子换成如图长为3cm，宽为2cm，高为1cm的长方体，蚂蚁沿着表面需要爬行的最短路程又是多少呢？AB分析：蚂蚁由A爬到B过程中较短的路线有多少种情况？(1)经过前面和上底面;(2)经过前面和右面;(3)经过左面和上底面.AB23AB1C321BCA321BCA(1)当蚂蚁经过前面和上底面时，如图，最短路程为223318解:AB23AB1C22BCACAB＝＝＝(2)当蚂蚁经过前面和右面时，如图，最短路程为22BCAC221526AB321BCAAB＝＝＝(3)当蚂蚁经过左面和上底面时，如图，最短路程为AB22BCAC222420262018cm2318即最短路程为AB＝＝＝321BCA2.在运用勾股定理时，我们必须首先明确哪两条边是直角边，哪一条是斜边.3.数学来源与生活，同时又服务于我们的生活.数学就在我们的身边，我们要能够学以致用.1.运用勾股定理解决实际问题,关键在于“找”到合适的直角三角形.小结作业1.必做题：课本123页习题14.2第1、2、3题.2.选做题:在一棵树的10米高处B有两只猴子，其中一只猴子爬下树走到离树20米的池塘A，另一只猴子爬到树顶D后直接跃向池塘的A处，如果两只猴子所经过距离相等，试问这棵树有多高？.DBCA