第三课时动量守恒定律应用VIP免费

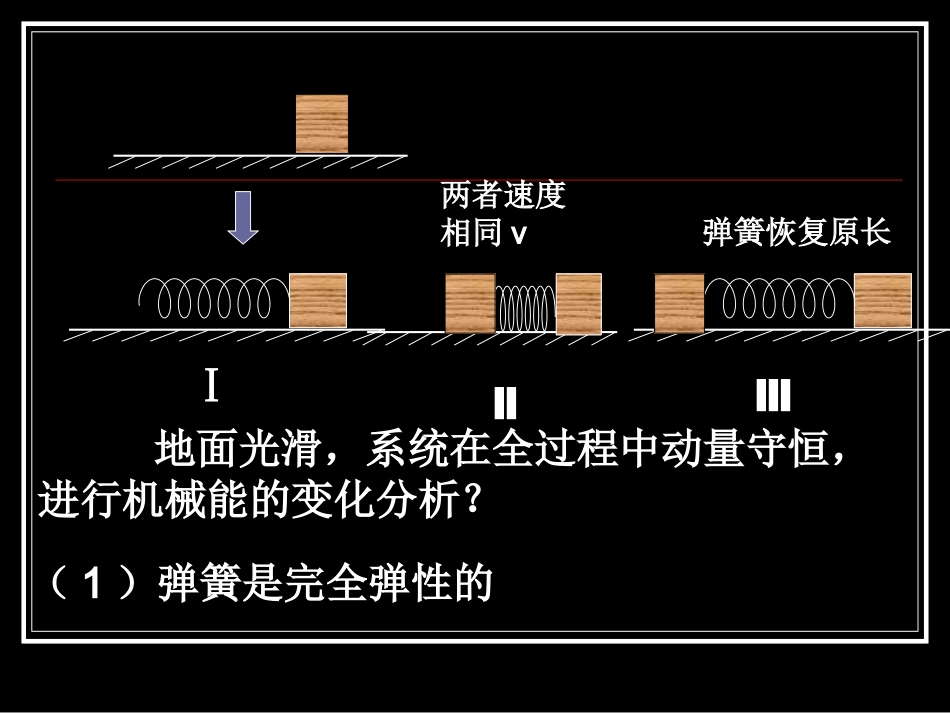
一、碰撞：1、定义：两个物体在极短时间内发生相互作用，这种情况称为碰撞。2、特点：3、分类：由于作用时间极短，一般都满足内力远大于外力，所以可以认为系统的动量守恒。弹性碰撞、非弹性碰撞、完全非弹性碰撞三种。4、过程分析：ⅠⅡⅢ两者速度相同v弹簧恢复原长地面光滑，系统在全过程中动量守恒，进行机械能的变化分析？（1）弹簧是完全弹性的Ⅰ→Ⅱ系统动能减少全部转化为弹性势能动能减少，弹性势能增加。Ⅱ状态动能最小而弹性势能最大Ⅱ→Ⅲ状态弹性势能减少全部转化为动能因此Ⅰ、Ⅲ状态系统动能相等这种碰撞叫做弹性碰撞（2）弹簧不是完全弹性的Ⅰ→Ⅱ系统动能减少，一部分转化为弹性势能，一部分转化为内能，Ⅱ状态系统动能仍和⑴相同，弹性势能仍最大，但比⑴小；Ⅱ→Ⅲ弹性势能减少，部分转化为动能，部分转化为内能；因为全过程系统动能有损失（一部分动能转化为内能）。这种碰撞叫非弹性碰撞。（3）弹簧完全没有弹性。Ⅰ→Ⅱ系统动能减少全部转化为内能，Ⅱ状态系统动能仍和⑴相同，但没有弹性势能；由于没有弹性，A、B不再分开，而是共同运动，不再有Ⅱ→Ⅲ过程。这种碰撞叫完全非弹性碰撞。（一）弹性碰撞特点：碰撞过程中，动量守恒，机械能守恒。两个方程：2'222'11222211'22'11221121212121vmvmvmvmvmvmvmvm121121212112,vmmmvvmmmmv121121212112,vmmmvvmmmmv121121212112,vmmmvvmmmmv121121212112,vmmmvvmmmmv解得：讨论：021120212112VmmmVVmmmmV1.若m1=m20102VVV质量相等的两物体弹性碰撞后交换速度2.若m1<>m202012VVVV1.物块m1滑到最高点位置时，二者的速度；2.物块m1从圆弧面滑下后，二者速度3.若m1=m2物块m1从圆弧面滑下后，二者速度如图所示，光滑水平面上质量为m1=2kg的物块以v0=2m/s的初速冲向质量为m2=6kg静止的光滑圆弧面斜劈体。求：例1v0m2m1解：（1）由动量守恒得m1V0=（m1+m2）VV=m1V0/（m1+m2）=0.5m/s（2）由弹性碰撞公式smVmmmVsmVmmmmV/1262222/12626202112021211（3）质量相等的两物体弹性碰撞后交换速度∴v1=0v2=2m/s【例1】质量为M的楔形物块上有圆弧轨道，静止在水平面上。质量为m的小球以速度v1向物块运动。不计一切摩擦，圆弧小于90°且足够长。求小球能上升到的最大高度H和物块的最终速度v。V1gmMMvH221gmMMvH22112vmMmv例3、质量相等的A、B两球在光滑水平面上沿同一直线，同一方向运动，A球动量为7kg·m/s，B球的动量为5kg·m/s，当A球追上B球时发生碰撞，则碰后A、B两球的动量PA、PB可能值是（）A、PA=6kg·m/sPB=6kg·m/sB、PA=3kg·m/sPB=9kg·m/sC、PA=-2kg·m/sPB=14kg·m/sD、PA=-4kg·m/sPB=17kg·m/sA③碰前、碰后两个物体的位置关系（不穿越）和速度大小应保证其顺序合理。方法归纳：①碰撞中系统动量守恒；②碰撞过程中系统动能不增加；（二）完全非弹性碰撞特点：碰撞后二者合二为一，或者说具有相同的速度。动量守恒，机械能损失最多。121121vmmmvv21212122121122121mmvmmvmmvmEk(三)非弹性碰撞介于两者之间。动量守恒，机械能有损失。如图所示，在光滑的水平面上，有一质量为m1=20千克的小车，通过几乎不可伸长的轻绳与质量m2=25千克的足够长的拖车连接。质量为m3=15千克的物体在拖车的长平板上，与平板间的摩擦系数=0.2，开始时，物体和拖车静止，绳未拉紧，小车以3米/秒的速度向前运动。求：(a)三者以同一速度前进时速度大小。(b)到三者速度相同时，物体在平板车上移动距离。例4m1m2m3v0二、子弹打木块类问题二、子弹打木块类问题下面从动量、能量和牛顿运动定律等多个角度来分析这一过程。1、问题实质：实际上是一种完全非弹性碰撞。2、特点：子弹以水平速度射向原来静止的木块，并留在木块中跟木块共同运动。例4、设质量为m的子弹以初速度v0射向静止在光滑水平面上的质量为M的木块，并留在木块中不再射出，子弹钻入木块深度为d。求木块对子弹的平均阻力的大小和该过程中木块前进的...