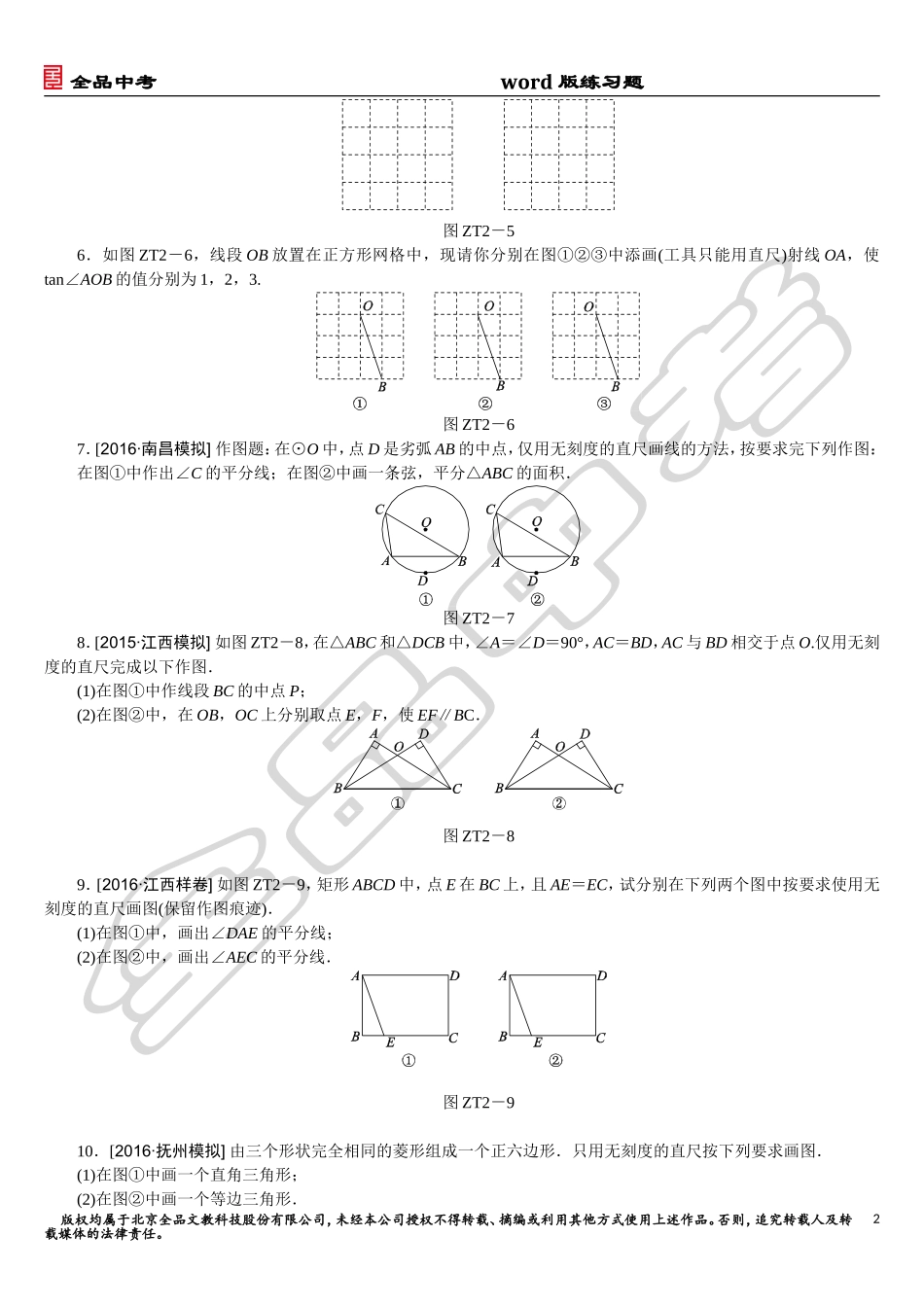
全品中考word版练习题专题训练(二)[创新作图题]1.[2016·鹰潭联考]用无刻度的直尺作图,保留作图痕迹,分别作出图中∠AOB的平分线:(1)如图ZT2-1①,∠AOB的两边与一圆切于点A、B,点M、N是优弧AB的三等分点;(2)如图②,∠AOB的两边与一圆交于点A、B、M、N,且AM=BN.图ZT2-12.[2016·吉安模拟]在▱ABCD中,点E在AD上,DE=CD,请仅用无刻度的直尺,按要求作图(保留作图痕迹,不写作法).(1)在图ZT2-2①中,画出∠C的平分线;(2)在图②中,画出∠A的平分线.图ZT2-23.[2016·江西样卷]如图ZT2-3,请仅用无刻度的直尺按下列要求画图:(1)如图①,在△ABC中,AB=AC,M、N分别是边AB、AC上的两点,且BM=CN,请画出线段BC的垂直平分线;(2)如图②,在菱形ABCD中,∠B=60°,E是AB边的中点,请画出线段BC的垂直平分线.图ZT2-34.[2014·江西样卷一]如图ZT2-4①中,弦AB∥CD,AB=CD,图②中,弦AB∥CD,AB≠CD,请仅用无刻度的直尺按要求画图.(1)在图①中,画出⊙O的圆心O;(2)在图②中,画出⊙O的一条直径.图ZT2-45.如图ZT2-5,正方形网格中的每个小正方形的边长都是1,每个小格的顶点叫做格点,在两个网格中分别以格点为顶点作出两个不全等的直角三角形,使它的两条直角边的长均为无理数,且较小锐角的正切值为.版权均属于北京全品文教科技股份有限公司,未经本公司授权不得转载、摘编或利用其他方式使用上述作品。否则,追究转载人及转载媒体的法律责任。1全品中考word版练习题图ZT2-56.如图ZT2-6,线段OB放置在正方形网格中,现请你分别在图①②③中添画(工具只能用直尺)射线OA,使tan∠AOB的值分别为1,2,3.图ZT2-67.[2016·南昌模拟]作图题:在⊙O中,点D是劣弧AB的中点,仅用无刻度的直尺画线的方法,按要求完下列作图:在图①中作出∠C的平分线;在图②中画一条弦,平分△ABC的面积.图ZT2-78.[2015·江西模拟]如图ZT2-8,在△ABC和△DCB中,∠A=∠D=90°,AC=BD,AC与BD相交于点O.仅用无刻度的直尺完成以下作图.(1)在图①中作线段BC的中点P;(2)在图②中,在OB,OC上分别取点E,F,使EF∥BC.图ZT2-89.[2016·江西样卷]如图ZT2-9,矩形ABCD中,点E在BC上,且AE=EC,试分别在下列两个图中按要求使用无刻度的直尺画图(保留作图痕迹).(1)在图①中,画出∠DAE的平分线;(2)在图②中,画出∠AEC的平分线.图ZT2-910.[2016·抚州模拟]由三个形状完全相同的菱形组成一个正六边形.只用无刻度的直尺按下列要求画图.(1)在图①中画一个直角三角形;(2)在图②中画一个等边三角形.版权均属于北京全品文教科技股份有限公司,未经本公司授权不得转载、摘编或利用其他方式使用上述作品。否则,追究转载人及转载媒体的法律责任。2全品中考word版练习题图ZT2-1011.如图ZT2-11所示,在8×8的网格中,我们把△ABC在图①中作轴对称变换,在图②中作旋转变换.已知网格中的线段DE、线段MN分别是边AB经两种不同变换后所得的像,请在两图中分别画出△ABC经各自变换后的像,并标出对称轴和旋转中心(要求:不写作法,作图工具不限,但要保留作图痕迹).图ZT2-1112.[2015·江西样卷一]图ZT2-12是以两个大小不同的正方形为基本图案镶嵌而成的图形,请仅用无刻度的直尺按不同的方法分别在图①、图②中画一个正方形,使它的面积等于这两个大小不同的正方形的面积之和.要求:(1)用虚线连接;(2)要标注你所画正方形的顶点字母.图ZT2-12版权均属于北京全品文教科技股份有限公司,未经本公司授权不得转载、摘编或利用其他方式使用上述作品。否则,追究转载人及转载媒体的法律责任。3全品中考word版练习题参考答案1.解:如图所示.2.解:(1)连接CE,由DE=DC得到∠DEC=∠DCE,由AD∥BC得∠DEC=∠BCE,则∠DCE=∠BCE,即CE平分∠BCD,如图①,CE为所作.(2)连接AC、BD,它们相交于点O,延长EO交BC于F,则AF为所作,如图②.3.解:(1)连接CM和BN,它们相交于点O,利用三角形全等可证明OB=OC,而AB=AC,则直线AO垂直平分BC,如图①,AD为所作;(2)连接BD、AC相交于点O,连接CE交BO于P,根据菱形的性质和等边三角形的判定与性质可判断CE和BO为等边△ABC的...