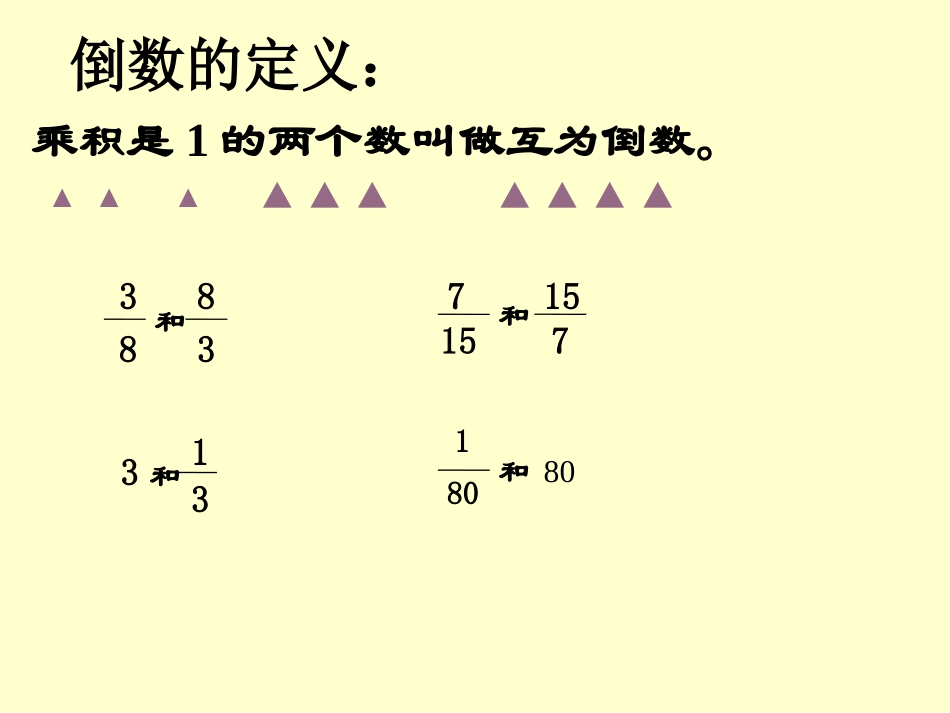
制作:李爱芳沙河市特殊教育学校每组中两个数的分子和分母都调换了位置。每组中的两个数相乘,积都等于1。观察下面的算式,你有什么发现?×3883=×715157=×313=1111×180=80乘积是1的两个数叫做互为倒数。倒数的定义:▲▲▲▲▲▲▲▲▲▲和3883和715157和313和18080—3—83×8=1倒数的表示:3883和互为倒数38是83的倒数38的倒数是83和313和715157↓↓和715157互为倒数的倒数是715157是715157的倒数和313互为倒数313的倒数是是313的倒数(2)只能说一个数是另一个倒数,或者说一个数和另一个数互为倒数。注意两点:(1)“互为倒数”是对两个数来说的,它们之间是相互依存的,不能孤立地说某个数是倒数。求一个数的倒数,可以把这个数的分子、分母交换位置。怎样求一个数的倒数?—53分子、分母调换位置—35—27—72的倒数是__53__35的倒数是__72__27求一个数的倒数时,必须用语言文字叙述,不能用等号连接。求一个数()的倒数,可以把这个数的分子、分母调换位置。0除外知识点拨:1的倒数是1。1×()=11想一想:1的倒数是多少?0×()=1因为0×≠1﹙﹚,任何数所以0没有倒数。0有倒数吗?如果有是多少?如果没有,举例说明理由。延伸:1.怎样求整数(0除外)的倒数?6先化成分母是1分数—16再调换分子、分母的位置__616的倒数是__61延伸:2.怎样求带分数的倒数?先化成假分数再调换分子、分母的位置__283的倒数是__283__819__819__198延伸:3.怎样求小数的倒数?0.75先化成分数再调换分子、分母的位置__430.75的倒数是__34__34课堂练习1写出下面各数的倒数。411169135780.25课堂练习2:下面哪两个数互为倒数?436718348561拓展练习判断(正确的在括号中画√,错误的画×)1、任意一个数都有倒数。()×2、a是一个自然数,它的倒数是()1a▁×3、乘积是1的两个数叫做互为倒数。()√4、0.3的倒数是3。()×5、因为=1所以互为倒数。()13▁23▁+13▁23▁和×