三角形四心的向量表示VIP免费

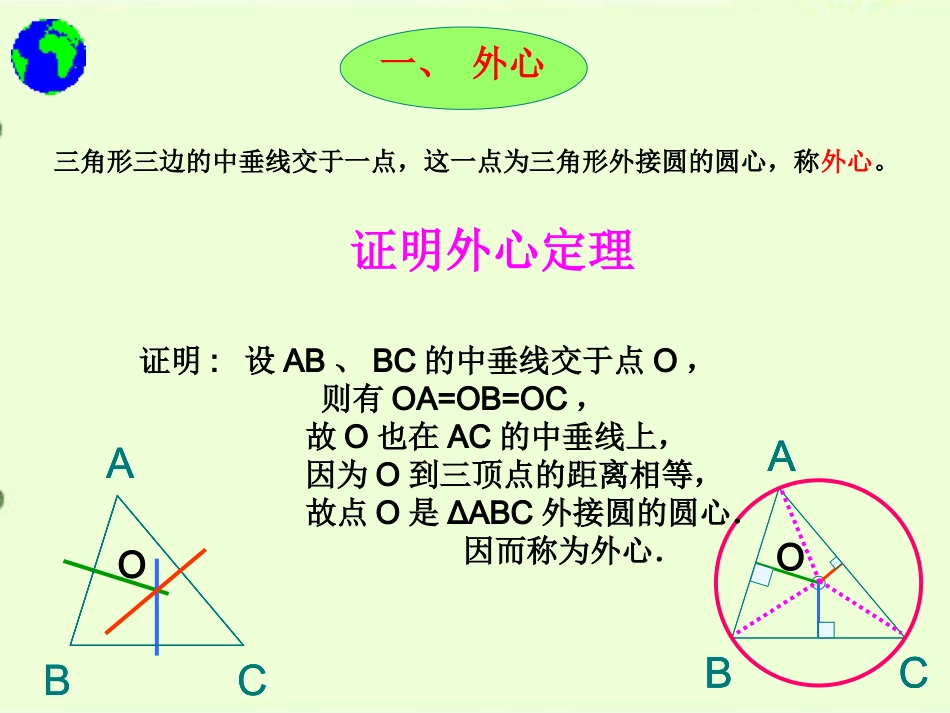
三角形“四心”的向量表示一、外心ABCABCABCABCABCABCABC三角形三边的中垂线交于一点，这一点为三角形外接圆的圆心，称外心。证明外心定理证明:设AB、BC的中垂线交于点O，则有OA=OB=OC，故O也在AC的中垂线上，因为O到三顶点的距离相等，故点O是ΔABC外接圆的圆心．因而称为外心．OO点评：本题将平面向量模的定义与三角形外心的定义及性质等相关知识巧妙结合。OABCOABC到的三顶点距离相等。故是解析：由向量模的定义知的外心，选B。ABCO是的外心OABCOAOBOC�OABC若为内一点，则是的（）A．内心B．外心C．垂心D．重心222OAOBOCOAOBOC��()()()OAOBABOBOCBCOCOACA�0B二、垂心ABCABCABC三角形三边上的高交于一点，这一点叫三角形的垂心。DEF证明:AD、BE、CF为ΔABC三条高，过点A、B、C分别作对边的平行线相交成ΔA′B′C′，AD为B′C′的中垂线；同理BE、CF也分别为A′C′、A′B′的中垂线，由外心定理，它们交于一点，命题得证．证明垂心定理A′B′C′例1．如图，AD、BE、CF是△ABC的三条高，求证：AD、BE、CF相交于一点。ABCDEFH,BHACCHAB�()0()()()0.()0habhabhbahbahba.AHBC�又 点D在AH的延长线上，∴AD、BE、CF相交于一点．,,,ABaACbAHh�令,,,BHhaCHhbBCba�则证：设BE、CF交于一点H，垂心ABCO,,,:,,.OAaOBbOCcBCcbCAabABba�则证：设例2．已知O为⊿ABC所在平面内一点，且满足:,,.ABOCBCOACAOB�求证：222222||||||||||||.OABCOBCAOCAB�化简：222222:||||||||||||.OABCOBCAOCAB�由题设222222()()()acbbaccba同理：,.BCOACAOB�()0,ABOCbacbcac�从而:cbacba得.ABOC�垂心ABCOAOCOCOBOBOA1.O是的垂心2.()||cos||cosABACABBACC��[0,)是△ABC的边BC的高AD上的任意向量，过垂心.12例3．O是平面上一定点，A、B、C是平面上不共线的三个点，动点P满足(),||cos||cosABACOPOAABBACC���()||cos||cos||cos||cosABACBCABBCACBCABBACCABBACC���||||cos()||||cos||||0||cos||cosBCABBBCACCBCBCABBACC���()||cos||cosABACBCABBACC���()||cos||cosABACABBACC��()||cos||cosABACOPOAABBACC���新疆源头学子小屋特级教师王新敞http://www.xjktyg.com/wxc/wxckt@126.comwxckt@126.comhttp://www.xjktyg.com/wxc/王新敞特级教师源头学子小屋新疆则P的轨迹一定通过△ABC的_______ ∴∴在△ABC的边BC的高AD上.P的轨迹一定通过△ABC的垂心.所以，时，解:OCOBOBOA解:例4.（2005全国Ⅰ）点O是ΔABC所在平面上一点，若，则点O是ΔABC的（）（A）三个内角的角平分线的交点（B）三条边的垂直平分线的交点（C）三条中线的交点（D）三条高线的交点OAOCOCOBOBOA0)(OCOAOB0CAOBCAOB则O在CA边的高线上,同理可得O在CB边的高线上.DOCBA垂心5.(2005湖南)P是△ABC所在平面上一点，若则P是△ABC的（）A．外心B．内心C．重心D．垂心,PAPBPBPCPCPA�D设中线BE,CF交于点G,连结EF,则EF//BC,且EF:BC=FG:GC=EG:GB=1:2.同理中线AD,BE交于G,连结DE,则:DE//AB,且EG:GB=DG:GA=DE:AB=1:2,故G(,证明同一法:)G重合.三、重心ABCABCABC三角形三边中线交于一点，这一点叫三角形的重心。证明重心定理EFDGABC0OCOBOA3.O是的重心14.()3PGPAPBPC�GABC为的重心.1.(),[0,)ABAC�是BC边上的中线AD上的任意向量，过重心.ABC1,2ADABAC�ABC2.在中，给出等于已知AD是中BC边的中线;1()3PGPAPBPC�例1．P是△ABC所在平面内任一点.G是△ABC的重心CGPCBGPBAGPAPG...