函数单调性课件VIP免费

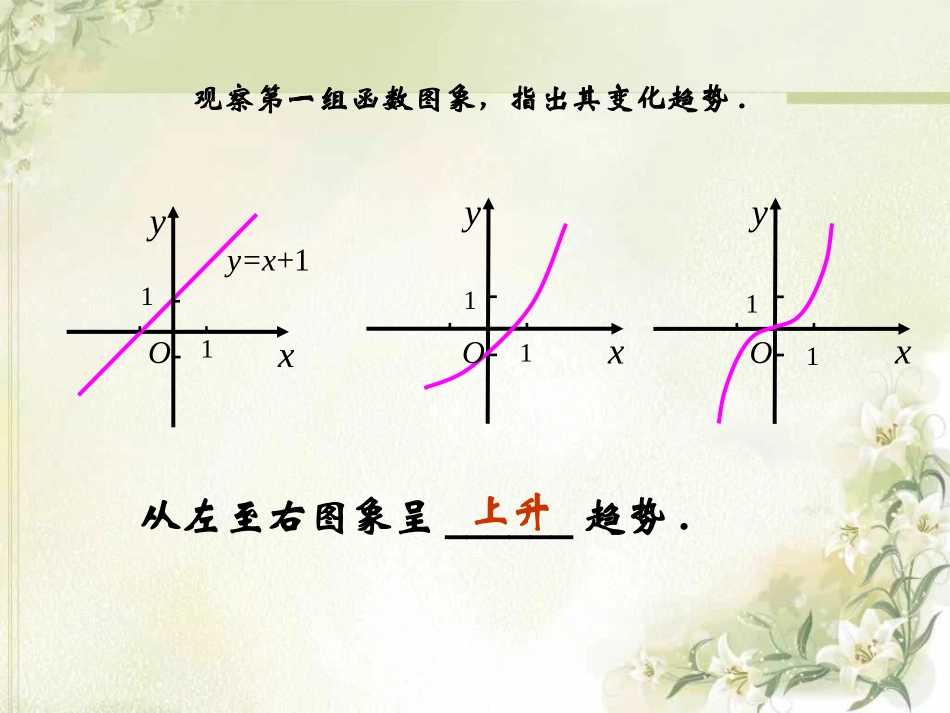
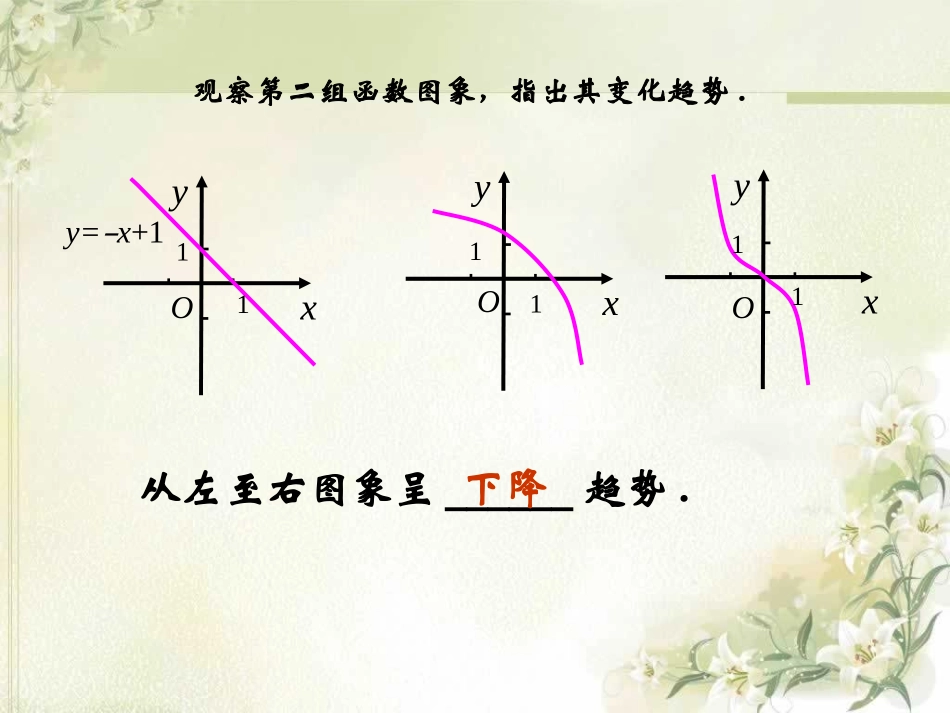
函数的单调性2011级4班2011060305邓晓曼xy从左至右图象呈______趋势.上升xyy=x+1xy观察第一组函数图象，指出其变化趋势.OOO111111y=-x+1xy从左至右图象呈______趋势.下降xyxy观察第二组函数图象，指出其变化趋势.OOO111111xyy=x2y从左至右图象呈______________趋势.局部上升或下降观察第三组函数图象，指出其变化趋势.xxy11-1-1OOO1111图像从左到右逐渐上升图像从左到右逐渐下降自变量x增大,自变量x增大,在定义域内的某个区间上因变量y也增大因变量y反而减小函数单调性定义:函数，定义域为A，区间()yfxIA如果在区间I内随着自变量的增大，因变量也增大，那么我们称在区间I上单调增，也称在区间I上是增函数xy如果在区间I内随着自变量的增大，因变量减小，那么我们称在区间I上单调减，也称在区间I上是减函数xy对区间I内x1，x2，当x1减减那么就说在f(x)这个区间上是函数，I称为f(x)的单调区间.增增单调区间判断2：函数f(x)在区间[1，2]上满足f(1)＜f(2)，则函数f(x)在[1，2]上是增函数.()yxO12f(1)f(2)判断1：函数f(x)=x2在是单调增函数；(),xyo2yx（1）函数单调性是针对定义域A内的某个子区间I而言的，是一个局部性质,在整个定义域上不一定具有单调性;（2）、在区间I内取任意值，不能用特殊值来代替.1x2x××要点解析：1、“定义域A内某个区间I”，即说明函数的单调区间是其定义域的子集；2、增、减函数定义中的,有三个特征：（1）、任意性，即不能用特殊值代替；（2）、有大小，通常规定<；（3）、属于同一区间。1x2x1x2x3、自变量取值之间的不等关系和函数值的不等关系正逆互推，即)(xf若是增函数，则2121)()(xxxfxf若是减函数，则)(xf2121)()(xxxfxf()yfx例题1：根据图像指出单调增区间和单调减区间单调增区间是：单调减区间是：[2,1],[3,5][5,2],[1,3]例2.指出下列函数的单调区间：(1)72yx(1)72yx的单调增区间是(2)24yx(2)24yx的单调减区间是解：),(),(无单调减区间无单调增区间归纳：函数的单调性(0)ykxbk单调增区间单调减区间k>0bkxy),(k<0),(yox272y=7x+22o4yxy=-2x+4归纳：函数的单调性2(0)yaxbxca2(1)2.yx2yx+2的单调增区间是_______;(,0]2yx+2的单调减区间是_______.[0,)例3.指出下列函数的单调区间：xyy=-x2+21-1122-1-2-2O2(2)2.yx思考2：函数的单调区间呢？223yxx思考1：函数的单调区间呢？2(1)2yx解：(1)单调增区间单调减区间2yaxbxc,2ba,2ba2(0)yaxbxca的对称轴为2bxa,2ba,2baa>0a<0例4.指出下列函数的单调区间：1yx1yx的单调减区间是_____________(,0)(0,),1(,0)(0,)yx能不能说在定义域上是单调减函数?x1yxyO思考1：思考2：函数的单调区间是什么？1yx1yx的单调增区间是),0(),0,(归纳：在和上的单调性？0,(0)kykx,0...