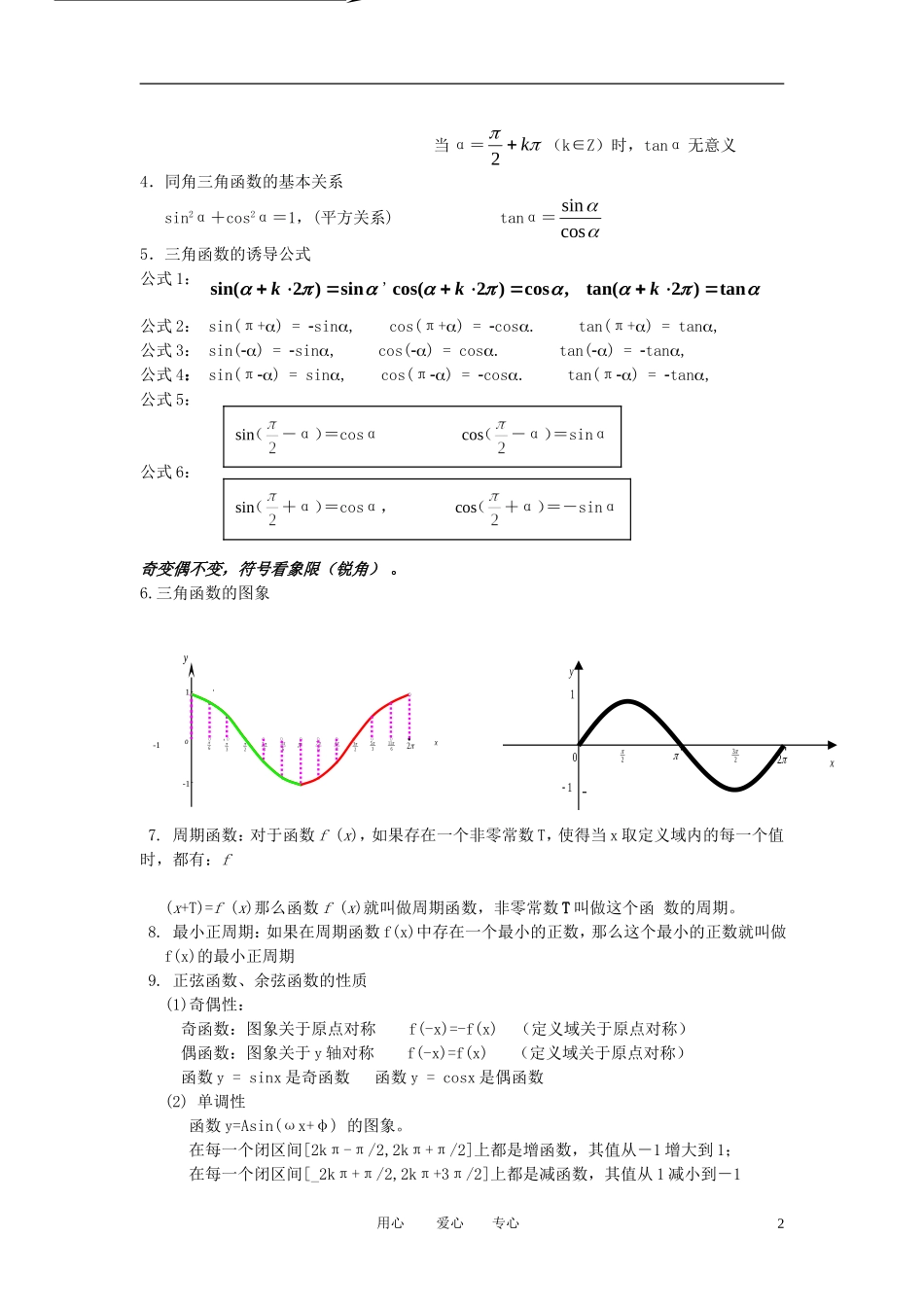
高考专题复习——三角函数、三角恒等变换、解三角形一考试要求(2011年普通高等学校招生全国统一考试安徽卷考试说明·文科数学)1.任意角、弧度(1)了解任意角的概念和弧度制的概念。(2)能进行弧度与角度的互化。2.三角函数(1)理解任意角三角函数(正弦、余弦、正切)的定义。(2)能利用单位圆中的三角函数线推导出的正弦、余弦、正切的诱导公式,能画出的图像,了解三角函数的周期性。(3)理解正弦函数、余弦函数在[0,2]上的性质(如单调性、最大值和最小值、图像与x轴的交点等),理解正切函数在内的单调性。(4)理解同角三角函数的基本关系式:(5)了解函数的物理意义;能画出函数的图像。了解参数对函数图像变化的影响。(6)会用三角函数解决一些简单实际问题,了解三角函数是描述周期变化现象的重要函数模型。3.两角和与差的三角函数公式(1)会用向量的数量积推导出两角差的余弦公式。(2)会用两角差的余弦公式推导出两角差的正弦、正切公式。(3)会用两角差的余弦公式推导出两角和的正弦、余弦、正切公式和二倍角的正弦、余弦、正切公式,了解它们的内在联系。4.简单的三角恒等变换能运用上述公式进行简单的恒等变换(包括导出积化和差、和差化积、半角公式,但不要求记忆)。5.正弦定理和余弦定理掌握正弦定理、余弦定理,并能解决一些简单的三角形度量问题。6.应用能够运用正弦定理、余弦定理等知识和方法解决一些与测量和几何计算有关的实际问题。二基础知识1、终边相同的角与α角终边相同的角,都可用式子k×360°+α表示2、弧度制.:半径为r的圆心角α所对弧长为l,则α弧度数的绝对值为|α|=lr.3.任意角的三角函数在直角坐标系中,设α是一个任意角,α终边上任意一点P(除了原点)的坐标为(,)xy,它与原点的距离为2222(||||0)rrxyxy,那么sin=yr,cosxr,tanyx用心爱心专心1yP(x,y)xr当α=k2(k∈Z)时,tanα无意义4.同角三角函数的基本关系sin2α+cos2α=1,(平方关系)tanα=cossin5.三角函数的诱导公式公式1:sin)2sin(k,tan)2tan(,cos)2cos(kk公式2:sin(π+)=sin,cos(π+)=cos.tan(π+)=tan,公式3:sin()=sin,cos()=cos.tan()=tan,公式4:sin(π)=sin,cos(π)=cos.tan(π)=tan,公式5:公式6:奇变偶不变,符号看象限(锐角)。6.三角函数的图象7.周期函数:对于函数f(x),如果存在一个非零常数T,使得当x取定义域内的每一个值时,都有:f(x+T)=f(x)那么函数f(x)就叫做周期函数,非零常数T叫做这个函数的周期。8.最小正周期:如果在周期函数f(x)中存在一个最小的正数,那么这个最小的正数就叫做f(x)的最小正周期9.正弦函数、余弦函数的性质(1)奇偶性:奇函数:图象关于原点对称f(-x)=-f(x)(定义域关于原点对称)偶函数:图象关于y轴对称f(-x)=f(x)(定义域关于原点对称)函数y=sinx是奇函数函数y=cosx是偶函数(2)单调性函数y=Asin(ωx+φ)的图象。在每一个闭区间[2kπ-π/2,2kπ+π/2]上都是增函数,其值从-1增大到1;在每一个闭区间[_2kπ+π/2,2kπ+3π/2]上都是减函数,其值从1减小到-1用心爱心专心2-oxy---11--13232656734233561126sin(+α)=cosα,cos(+α)=-sinαsin(-α)=cosαcos(-α)=sinα223xy0211---正弦函数y=cosx在每一个闭区间[2kπ-π,2kπ]上都是增函数,其值从-1增大到1;在每一个闭区间[2kπ,2kπ+π]上都是减函数,其值从1减小到-1正切xytan的递增区间是22kk,)(Zk,(3)最大值与最小值(对称轴)正弦函数当且仅当x=2kπ+π/2时取得最大值1,当且仅当x=2kπ+3π/2时取得最大值-1,sinyx的对称轴为2xk,对称中心为(,0)kkZ;余弦函数当且仅当x=2kπ时取得最大值1,当且仅当x=2kπ-π时取得最大值-1,cosyx的对称轴为xk,对称中心为2(,0)k;10.函数y=Asin(ωx+φ)的图象途径一:先平移变换再周期变换(伸缩变换)先将y=sinx的图象向左(>0)或向右(<0)平移||个单位,再将图象上各点...