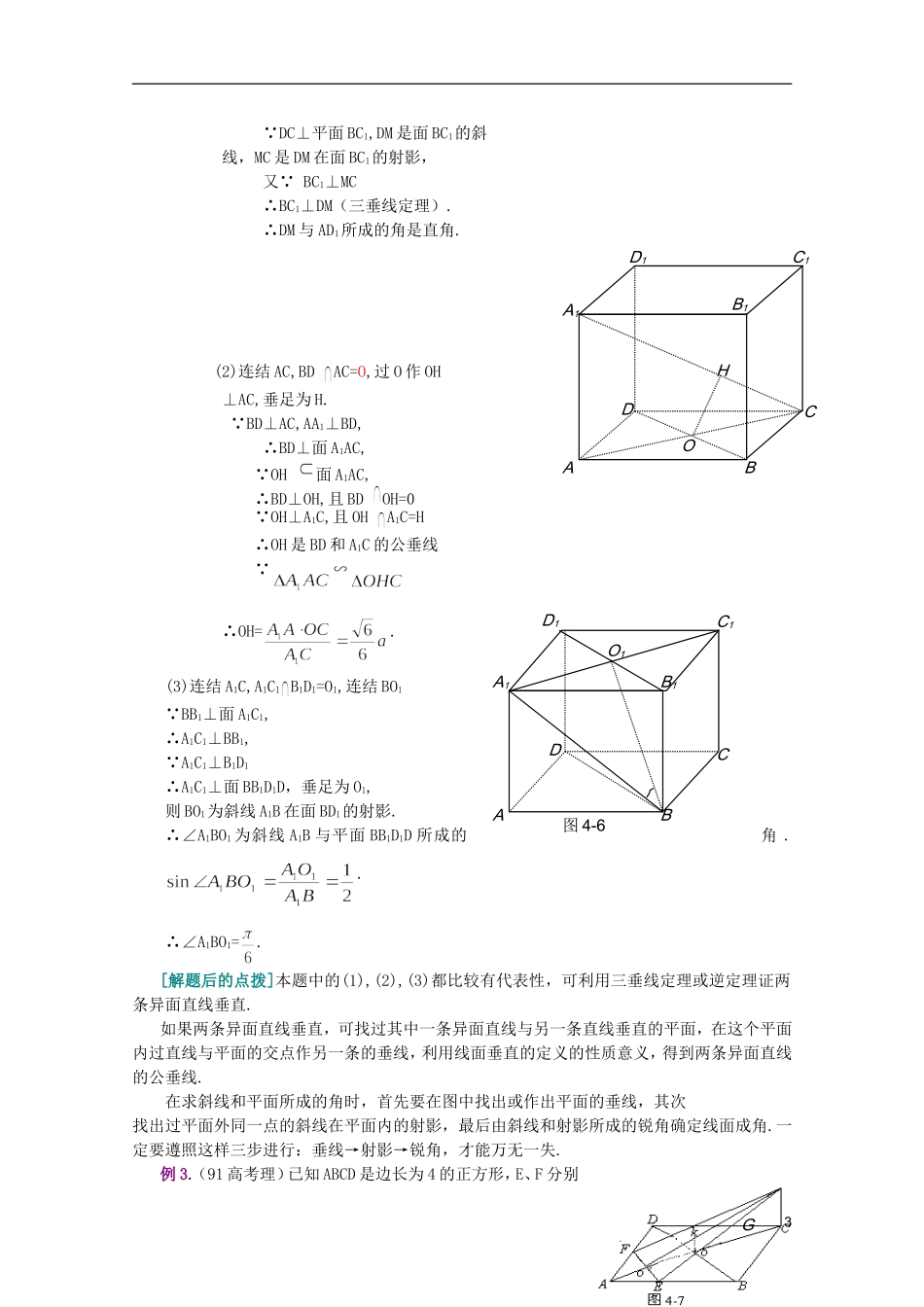
pababab直线与平面垂直的判定和性质[基础知识]定义直线和平面垂直判定性质若干概念平面的斜线直线和平面所成的角三垂线定理(逆定理)[学习指导]1.如何画直线和平面垂直?见书P23,如图4-12.你知道关于线面垂直的两个唯一性结论吗?过一点有且只有一条直线和已知平面垂直,过一点有且只有一个平面和已知直线垂直.3.如果一条直线上有两点和一个平面的距离相等,这条直线和平面的位置关系怎样?如果一条直线和一个平面平行,这条直线上各点到这个平面的距离相等,那么反过来,结论是否成立呢?显然不一定,如图4-24.如果两条直线和一个平面所成的锐角相等,那么这两条直线的位置关系如何?如果两条直线平行,则它们和同一个平面所成的角相等.但是反过来,结论就不一定成立,如图4-3,且均为锐角所以两条直线的位置关系有三种:相交,异面或平行.5.如何理解和运用三垂线定理及其逆定理?1图4-3P图4-1lASDBGFE图4-5C1B1A1MCDBAD1这两个定理都是研究直线和直线垂直关系的.所谓“三垂”是指三个垂直关系,如图4-4A为垂足.PO是的斜线,O为斜足则有AO⊥aPO⊥a要善于识别变式图形中定理所确定的直线和直线的垂直关系.首先要把一条直线看成是某一平面内的直线,另一条直线是这个平面的斜线或是某一条斜线在平面内的射影;其次是确定斜线上某一点所引的这个平面垂线和垂足;最后按定理条件得出两条直线的互相垂直.三垂线定理及其逆定理沟通线线、线面垂直间的关系,是立体几何中极其重要的定理.[例题精析]例1.如图4-5,ABCD为正方形,SA⊥平面ABCD,过A且垂直于SC的平面交SB、SC、SD分别于点E、F、G.求证:AE⊥SB.[分析]要证线线垂直,常把一条直线放在一个平面内证另一条直线垂直于这个平面,则垂直于这条直线,即要证线线垂直,去找线面垂直.[证明] SA⊥平面ABCD,BC面ABCD,∴SA⊥BC, 四边形ABCD是正方形,∴BC⊥AB,且ABSA=A,∴BC⊥面SAB,AE面SAB,∴BC⊥AE. SC⊥面AEFG,AE面AEFG,∴SC⊥AE,且BCSC=C,∴AE⊥面SBC,SB面SBC,∴AE⊥SB.[解题后的点拨]线线垂直和线面垂直的关系十分密切,常常在做题中互为题设互为结论,有如下关系:定义线面垂直线线垂直判定定理例2.如图4-6,正方体ABCD—A1B1C1D1中棱长为a,侧面BCC1B1的中心是M,求:(1)DM与AD1所成的角;(2)DB与A1C的距离;(3)A1B与对角面BB1D1D所成的角;[分析]本题求异面直线所成的角、距离、线面成角,先根据定义作出、证出所求的角或距离,再求值.[解](1) AD1//BC1,∴DM与AD1所成的角是DM与BC1所成的角,2逆定理定理CaPoA图4-4DCBAOHB1A1C1D1 DC⊥平面BC1,DM是面BC1的斜线,MC是DM在面BC1的射影,又 BC1⊥MC∴BC1⊥DM(三垂线定理).∴DM与AD1所成的角是直角.(2)连结AC,BDAC=O,过O作OH⊥AC,垂足为H. BD⊥AC,AA1⊥BD,∴BD⊥面A1AC, OH面A1AC,∴BD⊥OH,且BDOH=0 OH⊥A1C,且OHA1C=H∴OH是BD和A1C的公垂线 ∽∴OH=.(3)连结A1C,A1C1B1D1=O1,连结BO1 BB1⊥面A1C1,∴A1C1⊥BB1, A1C1⊥B1D1∴A1C1⊥面BB1D1D,垂足为O1,则BO1为斜线A1B在面BD1的射影.∴∠A1BO1为斜线A1B与平面BB1D1D所成的角..∴∠A1BO1=.[解题后的点拨]本题中的(1),(2),(3)都比较有代表性,可利用三垂线定理或逆定理证两条异面直线垂直.如果两条异面直线垂直,可找过其中一条异面直线与另一条直线垂直的平面,在这个平面内过直线与平面的交点作另一条的垂线,利用线面垂直的定义的性质意义,得到两条异面直线的公垂线.在求斜线和平面所成的角时,首先要在图中找出或作出平面的垂线,其次找出过平面外同一点的斜线在平面内的射影,最后由斜线和射影所成的锐角确定线面成角.一定要遵照这样三步进行:垂线→射影→锐角,才能万无一失.例3.(91高考理)已知ABCD是边长为4的正方形,E、F分别3B1A1DCBAD1C1O1图4-6Gaa′bA′┘图4-9是AB、AD的中点,GC垂直于ABCD所在的平面,且GC=2,求点B到平面EFG的距离,如图4-7.[分析]求点到平面的距离,可转化为平行线面的距离.[解]连结AC、BD,ACBD=O,ACEF=O′连结GO′,过O作OK⊥GO′. EF//BD,∴BD//平面EFG,点B到平面EFG的距离等于O点到平面EFG的距离. GC⊥平面ABCD,∴GC⊥EF, EF⊥AC,∴EF...