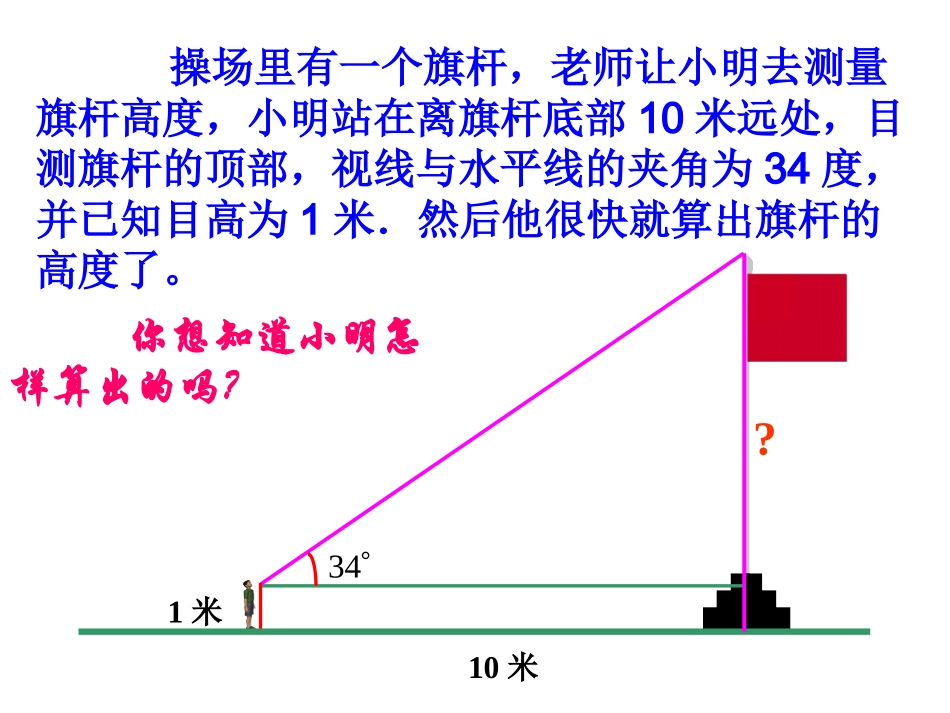
操场里有一个旗杆,老师让小明去测量旗杆高度,小明站在离旗杆底部10米远处,目测旗杆的顶部,视线与水平线的夹角为34度,并已知目高为1米.然后他很快就算出旗杆的高度了。1米3410米?你想知道小明怎样算出的吗?我们已经知道,直角三角形ABC可以简记为RtABC△,直角∠C所对的边AB称为斜边,用c表示,另两条直角边分别叫∠A的对边与邻边,用a、b表示.图19.3.1如图,在RtMNP△中,∠N=90゜.P∠的对边是__________,P∠的邻边是_______________;∠M的对边是__________,M∠的邻边是_______________;(第1题)MNPNPNMN想一想:∠P的对边、邻边与∠M的对边、邻边有什么关系?•观察图的RtAB△1C1、RtA△B2C2和RtAB△3C3,它们之间有什么关系?图19.3.2RtAB△1C1RtAB∽△2C2RtAB∽△3C3所以=__________=__________.111ACCB可见,在RtABC△中,对于锐角A的每一个确定的值,其对边与邻边的比值是惟一确定的.B2C2AC2B3C3AC3图19.3.2想一想对于锐角A的每一个确定的值,其对边与斜边、邻边与斜边、的比值也是惟一确定的吗?想一想结论:在Rt△ABC中,如果锐角A确定时,那么∠A的对边与斜边的比,邻边与斜边的比也随之确定.ABC∠A的对边∠A的邻边┌斜边对于锐角A的每一个确定的值,sinA有唯一确定的值与它对应,所以sinA是A的函数.当∠A=30°时,归纳总结:在直角三角形中,当锐角A的度数一定时,不管三角形的大小如何,∠A的对边与斜边的比是一个固定值.在RtABC△中,C=90∠0,把锐角A的对边与斜边的比叫做∠A的正弦(sine),ABC对边邻边┌斜边abc记作sinA.(sinBAC∠)∠A的对边斜边即sinA==acsinA=sin30°=当∠A=45°时,sinA=sin45°=2212ac1、sinA不是一个角2、sinA不是sin与A的乘积3、sinA是一个比值4、sinA没有单位注意:余弦在Rt△ABC中,锐角A的邻边与斜边的比叫做∠A的余弦,记作cosA,即ABC∠A对边a∠A邻边b┌斜边ccbAA=斜边的邻边cos想一想:cos45°=?cos30°=?讨论•若∠A为锐角,那么sinA、cosA的取值范围是什么?•试比较sinA+cosA与1的关系。•你知道sin2A+cos2A是多少吗?cbaBAC练一练1.判断对错:A10m6mBC1)如图(1)sinA=()(2)cosB=()(3)sinA=0.6m()(4)SinB=4/5()ABBCBCAB√√√×sinA是一个比值(注意比的顺序),无单位;2)如图,cosB=()BCAB×2.在Rt△ABC中,锐角A的对边和斜边同时扩大100倍,sinA的值()A.扩大100倍B.缩小C.不变D.不能确定C1100练一练3.如图ACB37300则sinA=___cosA=___.12练一练ABC513,135==sinABBCA4.如图,在RtABC△中,C=90°,AB=13,BC=∠5求sinA和sinB的值.解:在RtABC△中,,125-13-2222BCABAC.1312==sin∴ABACB求一个角的正弦值,除了用定义直接求外,还可以转化为求和它相等角的正弦值。如图,C=90°CDAB.∠⊥sinB可以由哪两条线段之比?想一想若AC=5,CD=3,求sinB、cosB的值.┌ACBD解:B=ACD∵∠∠∴sinB=sinACD∠在RtACD△中,AD=sinACD=∠∴sinB=222235=--CDAC54=ACAD54=4练习•在RtABC△中,∠C=90°,AB=5,AC=4,则sinA的值为_____。•在RtABC△中,∠C=90°,则下列关系不一定成立的是_______。A:sinA=cosBB:cosA=sinBC:sinA=sinBD:cosA=cosB•在RtABC△中,∠C=90°,若BC=2,sinA=则边AC的长是_____。A:B:3C:D:3451332要想使人安全地攀上斜靠在墙面上的梯子的顶端,梯子与地面所成的角α一般要满足0.77≤sinα≤0.97.现有一个长6m的梯子,问使用这个梯子能安全攀上一个5m高的平房吗?用一用12小结拓展1.锐角三角函数定义:2.sinA是∠A的函数.ABC∠A的对边┌斜边斜边∠A的对边sinA=3.若α为锐角,则0<sinα<1,0<cosα<1Sin300=sin45°=224、sin2A+cos2A=1