统计学一元线性回归课后习题答案VIP免费

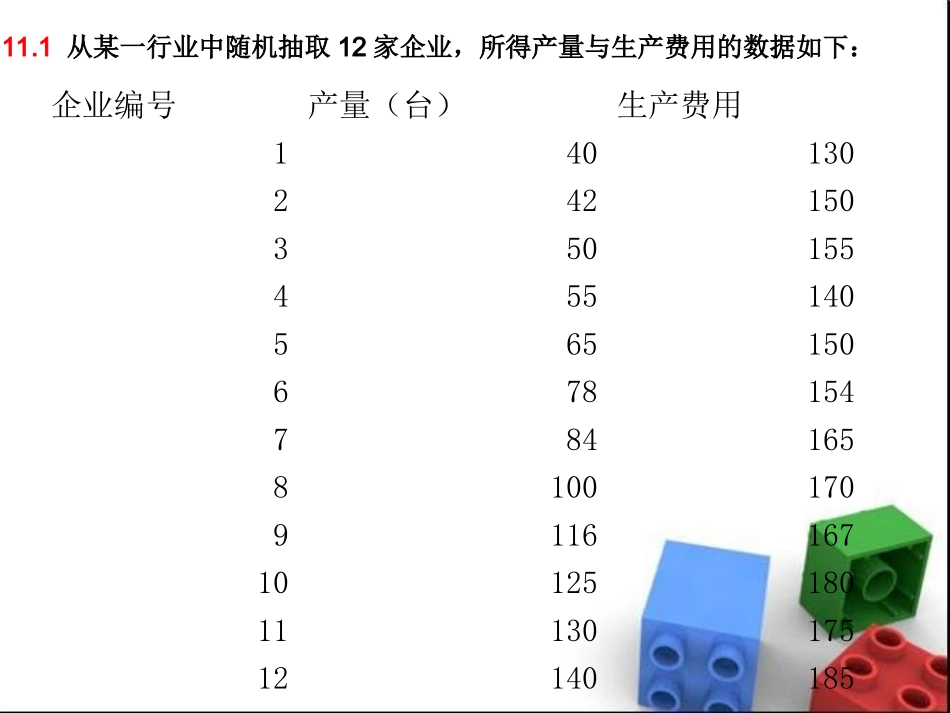
一元线性回归课后习题讲解--------第九组11.1从某一行业中随机抽取12家企业，所得产量与生产费用的数据如下：企业编号产量（台）生产费用14013024215035015545514056515067815478416581001709116167101251801113017512140185产量与生产费用020406080100120140160180200020406080100120140160产量费用系列1产量和费用存在正的线性相关系数（1）绘制产量与生产费用的散点图，判断二者之间的关系形态。r=0.92022222yynxxnyxxynr2222yynxxnyxxynr222222212(40*13042*150...140*185)(4042...140)*(130150...185)12*(4042...140)20162212*(130150...185)(130150...185)r2）计算产量与生产费用之间的线性相关系数。11、提出假设：、提出假设：HH00：：；；HH11：：002、计算检验的统计量)2(~122ntrnrt)2(~122ntrnrt根据显著性水平根据显著性水平＝＝0.050.05，查，查tt分布表得分布表得tt((nn--2)=2.22812)=2.2281由于由于tt=7.435453>=7.435453>tt(12-2)=2.2281(12-2)=2.2281，，拒绝拒绝HH00，产量与生产费用之间存在着显著的正线，产量与生产费用之间存在着显著的正线性相关关系性相关关系21220.92027.43545310.9202t（3）对相关系数的显著性进行检验（＝＝0.050.05),并说明二者之间的关系强度。tt(12-2)=2.2281(12-2)=2.228111.2学生在期末考试之前用于复习的时间（单位：小时）和考试分数（单位：分）之间是否有关系？为研究这一问题，一位研究者抽取了由8名学生构成的一个随机样本，取得的数据如下：复习时间X2016342327321822考试分数Y646184708892727701020304050607080901000510152025303540复习时间分数系列1复习时间和考试分数存在正的线性相关关系复习时间和考试分数存在正的线性相关关系复习时间和考试分数存在正的线性相关关系要求：（1）绘制复习时间和考试分数的散点图，判断二者之间的关系形态。r=0.86212222yynxxnyxxynr2222yynxxnyxxynr（2）计算相关系数，说明两个变量之间的关系强度。222222228(20*6416*61...22*77)(2016...22)*(6461...77)8*(2016...22)2016...228*(6461...77)(6461...77)r11.3、根据一组数据建立的线性回归方程要求：1）解释截距的意义。1）解释斜率的意义。2）当=6时的E（y）1）表示在没有自变量X的影响时其他各种因素对因变量Y的影响为102）斜率的意义在于：自变量X变化对Y影响程度。回归方程中，当x增加一个单位时,y将减少0.5个单位。3）x=6时，代入方程，则，y=10-0.56=7ˆˆ100.5yx1ˆ0ˆ11.4设SSR=36，SSE=4，n=18要求：1）计算判定系数R^2并解释其意义回归直线对观测值的拟合程度为0.9，说明变量Y的变异性中有90%是由自变量x引起的。2）计算估计标准误差并解释其意义es21ˆ40.5218216niiieyySSEsn2360.940SSRSSRRSSTSSTSSE表示实际值与估计值之间的差异程度是0.511.5一家物流公司的管理人员想研究货物的运输距离和运输时间的关系，为此，他抽出了公司最近10个卡车的运货记录的随机样本，得到运送距离（单位：km）和运送时间（单位：天）的数据如下表：运送距离x825215107055048092013503256701215运送时间y3.51.04.02.01.03.04.51.53.05.0(1)绘制运送距离和运送时间的散点图，判断二者之间的关系形态(2)计算线性相关系数，说明两个变量之间的关系强度。(3)利用最小二乘法求出估计的回归方程，并解释回归系数的实际意义。根据图表显示，二者可能存在正线性相关关系0.01.02.03.04.05.06.002004006008001000120014001600运送距离（公里）运送时间（天）(1)绘制运送距离和运送时间的散点图，判断二者之间的关系形态x与y的简单相关系数是0.9489，两变量之间呈现高度正相关关系运送距离x运送时间y运送距离x1运送时间y0.948941(2)计算线性相关系...