参数方程和普通方程的互化VIP免费

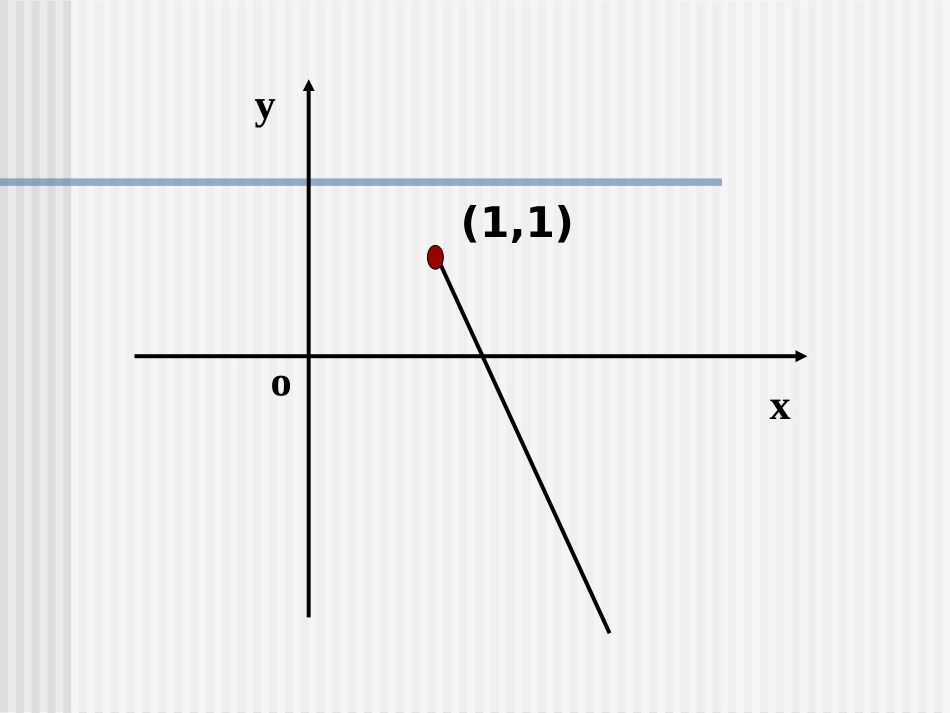
3、参数方程和普通方程的互化)(211{13为参数）（表示什么曲线？普通方程，并说明各、把下列参数方程化为例ttytx2sin1cossin{2yx）、（)()1,1()1(32,1132,211111包括端点为端点的一条射线这是以普通方程是所以与参数方程等价的又得到代入有）由解：（xxytxxytyxttxyxo(1,1)这是抛物线的一部分。普通方程为所以与参数方程等价的所以又得到平方后减去把].2,2[,],2,2[),4sin(2cossin,2sin1cossin)2(22xyxxxyxyx2sin1cossin{2yx）、（xoy22步骤：1、消掉参数(代入消元，三角公式法，配方法)2、写出定义域（x的范围）参数方程化为普通方程的步骤在参数方程与普通方程的互化中，必须使x,y前后的取值范围保持一致。注意：为参数）设（为参数。）设（的参数方程、求椭圆例ttyxyx,22,cos31149422)(sin2cos3{149,sin2sin2sin4)cos1(4,149cos9cos312222222为参数的参数方程是所以椭圆的任意性，可取由参数即所以代入椭圆方程，得到）把解：（yxyxyyyyxtytxttytxyxtxtxtxty213{)(213{14913),1(9144922222222222和为参数的参数方程是所以，椭圆于是代入椭圆方程，得）把（22{()yxxtAtyt练习:1.下列参数方程与方程表示同一曲线的是为参数)(sinsin{2为参数ttytxB)({为参数ttytxC)(tan2cos12cos1{为参数ttyttxD222.4,_________xyxy若则的最大值是222cos4{(2sin)xxyy解：的参数方程为为参数2cos2sin22cos()422xy最大值为2213.{()224199xttytxyABAB设直线的参数方程为为参数它与椭圆的交点为和，求线段的长度。2108744414)(187,207168)2()1()2.........(..........094)1...(..........42,0422122122121222xxxxkdxxxxxxyxxyyx由弦长公式得得代入将椭圆化为得到化为普通方程得解：将直线的参数方程小节1、将参数方程化为普通方程的方法2、将普通方程化为参数方程的方法注意：在参数方程与普通方程的互化中，必须使x,y的取值范围保持一致。作业：27页5题