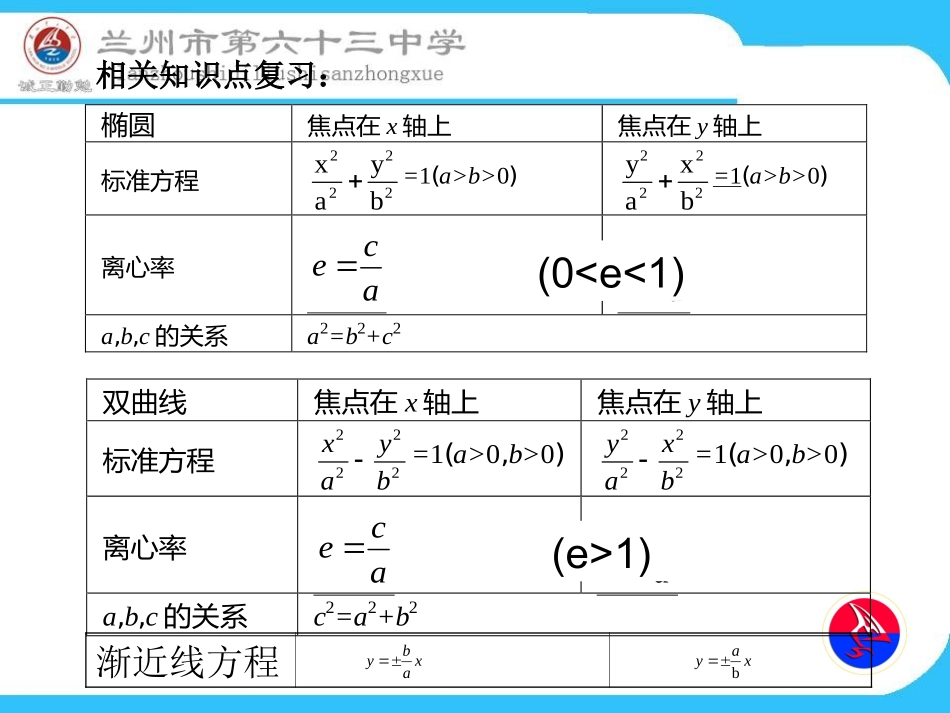
离心率的求法第一课时相关知识点复习:双曲线焦点在x轴上焦点在y轴上标准方程2222xyab=1(a>0,b>0)2222yxab=1(a>0,b>0)离心率aceacea,b,c的关系c2=a2+b2椭圆焦点在x轴上焦点在y轴上标准方程2222xyab=1(a>b>0)2222yxab=1(a>b>0)离心率aceacea,b,c的关系a2=b2+c2(01)渐近线方程xabyxayb例1、(2008、2010全国卷大题第一问变式)双曲线(a>0,b>0)实轴长、虚轴长、焦距成等差数列,则双曲线的离心率e=________.方法一:解方程组求离心率(方程法)12222byax35例2、(2010辽宁高考变式)双曲线的中心在坐标原点,左顶点和左焦点分别为A、F,虚轴的两个端点分别为和,如果,那么此双曲线的离心率为()(A)(B)(C)(D)23213215DB1B2BBFA12巩固练习:已知点F、A分别为双曲线(a>0,b>0)的左焦点、右顶点,点B(0,b)满足,则双曲线的离心率为____________.(2012河南郑州质量检测)0ABFB12222byax215例3、【2010新课标全国,5】中心在原点,焦点在x轴上的双曲线的一条渐近线经过(4,2),则它的离心率为()(A)(B)(C)(D)656252D方法二:(定义法)自主探究1、已知双曲线(a>0,b>0)的一条渐近线方程为,则双曲线的离心率为()A.B.C.D.2、(河北12年质量检测)已知焦点在x轴上的双曲线的渐近线方程是,则该双曲线的离心率是______.12222byaxxy34xy435453423A17巩固练习【2011新课标全国,4】椭圆的离心率为()A.B.C.D.221168xy13123322D(3)(4)椭圆中长轴长为短轴长的两倍,则离心率e=________.(5)椭圆中焦距与短轴长相等,则离心率e=________.232222832xy的实轴长_____,为虚轴长为_____,顶点坐标为___________,焦点坐标为________,离心率为______。224xy(7)的实轴长,虚轴长,顶点坐标为__________,焦点坐标为,离心率为______。4280,240,632444(0,±2)22,02(6)小结:1、解决问题的方法:第一课时定义法、方程法、第二课时几何法2、思想与收获:人生需要思考和感悟,有了这两者,人生才能变得睿智、快乐、和轻松!作业:1、完成导学案,特别注意作业1、2题2、在《优化训练》中总结相关题型3、探究离心率取值范围的题目作业1作业2作业3(山东高考)双曲线的两个顶点将焦距三等分,则它的离心率为_______。